-
Listen to a special audio message from Bill Roper to the Hive Workshop community (Bill is a former Vice President of Blizzard Entertainment, Producer, Designer, Musician, Voice Actor) 🔗Click here to hear his message!
-
Read Evilhog's interview with Gregory Alper, the original composer of the music for WarCraft: Orcs & Humans 🔗Click here to read the full interview.
-
Create a faction for Warcraft 3 and enter Hive's 19th Techtree Contest: Co-Op Commanders! Click here to enter!
-
Create a void inspired texture for Warcraft 3 and enter Hive's 34th Texturing Contest: Void! Click here to enter!
-
The Hive's 21st Texturing Contest: Upgrade is now concluded, time to vote for your favourite set of icons! Click here to vote!
Advanced Maths & Ingame Calculator
Advanced Mathematics & Ingame Calculator
vJass Version 1.2.0.0

1. Introduction
This is a math library designed to provide advanced mathematic functions and functionalities that are not supported by the World Editor. Mathematics are important for various things like calculating a units armor, physic systems with kinematics or differential equations, movement, artificial intelligence, statistics for balancing and many more. Therefore it is quite annoying that the World Editor lacks of many important math functions. The aim of this system is to close this gap - The library provides extremly efficient functions to calculate logarithms, hyperbolic functions and their inverses as well as typecheck or rounding functions and many more. Not only "complicated" functions are provided but also very easy ones like the absolute value of a real number, to finally have a full and complete list of important functions which every Math library should provide.
Further the library is designed modular, so that further and more advanced extensions can be easily added or removed from the system core. As a first Extension, there is a MathParser library included to the system which provides a fully functional interpreter for mathematic expressions, making it possible to implement an ingame calculator to the game. Further Plug-Ins or Extensions will follow.
2. System Code
Enclosed is the systems code. The system uses Newton-Cotes formulars to compute logarithms, hyperbolic functions and their inverses at an extremly high precision with a minimal overhead. Only four divisions are used in the worst case to compute the natural logarithm of a number, apart from that only additions and multiplications are used, making these functions very efficient. Some functions of the library already exist in the standard editor, like the min/max functions or abs. These are included for better readability to not have to use BJs. For more details about the interpreter, see section 3.
JASS:
library Maths/* v 1.2.0.0
**********************************************************************************
*
* Advanced Mathematics
* ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
* By looking_for_help aka eey
*
* This system provides a large amount of standard mathematical functions that
* miss in standard Jass like logarithmic, hyperbolic, typecheck or rounding
* functions. It can be extended with various optional libraries.
*
***********************************************************************************
*
* Requirements
* ¯¯¯¯¯¯¯¯¯¯¯¯
* */ uses ErrorMessage /* hiveworkshop.com/forums/jass-resources-412/snippet-error-message-239210/
*
***********************************************************************************
*
* Implementation
* ¯¯¯¯¯¯¯¯¯¯¯¯¯¯
* To use this system, just copy this script to your trigger editor, then you
* can use it straight away. To see how the evaluation function works, compare
* the example IngameCalculator trigger.
*
**********************************************************************************
*
* Available Plug-Ins and Extensions
* ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
* library MathParser
* - A library that allows you to parse string expressions. Compare the
* IngameCalculator Trigger for an example usage.
*
* library Matrices
* - A library that allows you to perform Matrix and Vector operations
* like solving a System of Linear Equations, compute the inverse of
* a Matrix, perform Matrix multiplication and so on.
*
**********************************************************************************
*
* System API
* ¯¯¯¯¯¯¯¯¯¯
* struct Math
* ¯ ¯ ¯ ¯ ¯ ¯
* readonly static real Pi
* - Refer to this field for the number Pi, the ratio of a circle's
* circumference to its diameter
*
* readonly static real E
* - Refer to this field for the number E, the base of the natural
* exponential function.
*
* readonly static real Phi
* - Refer to this field for the number Phi, the golden ratio.
*
* readonly static real Inf
* - Refer to this field for 2^128, the biggest real number Wc3 can
* handle. You can use -Math.Inf to get the smallest real number.
*
* readonly static integer MinInt
* - Refer to this field for -2147483648, the smallest integer number
* that Wc3 can handle.
*
* readonly static integer MaxInt
* - Refer to this field for 2147483647, the biggest integer number
* that Wc3 can handle.
*
* static method abs takes real r returns real
* - Computes the absolute value of a number.
*
* static method sig takes real r returns real
* - Extracts the sign of a real number.
*
* static method max takes real r1, real r2 returns real
* - Returns the bigger of two values r1 and r2.
*
* static method min takes real r1, real r2 returns real
* - Returns the smaller of two values r1 and r2.
*
* static method mod takes real r1, real r2 returns real
* - Computes the rest of the division r1/r2.
*
* static method modInt takes integer n1, integer n2 returns integer
* - Computes the modulo of n1/n2.
*
* static method multiMod takes integer n1, integer n2, integer mod returns integer
* - Computes the modulo of n1*n2/mod. Use this to compute the
* modulo of very large numbers.
*
* static method expMod takes integer x, integer n, integer modulo returns integer
* - Computes the modulo of x^n/modulo. Use this to compute the
* modulo of extremly large numbers.
*
* static method digits takes real r returns integer
* - Returns the number of digits before the comma of a given real number.
*
* static method isDigit takes string s returns boolean
* - Determines whether a string is a digit or not.
*
* static method isInteger takes real r returns boolean
* - Determines whether a real is integer or not.
*
* static method isEven takes real r returns boolean
* - Determines the parity of a real number.
*
* static method isPrime takes real r returns boolean
* - Determines whether a number is a prime or not by using a deterministic
* version of the Miller-Rabin test.
*
* static method sinh takes real r returns real
* - Computes the hyperbolic sine of a real number.
*
* static method cosh takes real r returns real
* - Computes the hyperbolic cosine of a real number.
*
* static method tanh takes real r returns real
* - Computes the hyperbolic tangent of a real number.
*
* static method asinh takes real r returns real
* - Computes the inverse hyperbolic sine of a real number.
*
* static method acosh takes real r returns real
* - Computes the inverse hyperbolic cosine of a real number.
*
* static method atanh takes real r returns real
* - Computes the inverse hyperbolic tangent of a real number.
*
* static method ln takes real r returns real
* - Computes the natural logarithm to a number by using Newton-Cotes.
* Reaches extremly high accuracies very efficiently. This method
* is used to compute all other logarithms and inverse hyperbolic
* functions.
*
* static method log2 takes real r returns real
* - Computes the binary logarithm to a number.
*
* static method log10 takes real r returns real
* - Computes the common logarithm to a number.
*
* static method log takes real r1, real r2 returns real
* - Computes the logarithm of a number r2 to the base r1.
*
* static method floor takes real r returns real
* - Rounds a number to the next smallest integer.
*
* static method ceil takes real r returns real
* - Rounds a number to the next largest integer.
*
* static method round takes real r returns real
* - Rounds a number to the nearest whole number.
*
* static method fractional takes real r returns real
* - Computes the fractional part of a number.
*
* static method mergeFloat takes real r returns real
* - Merges the fracional and the non fractional parts of a number
* together to an integer number.
*
* static method factorial takes real r returns real
* - Computes the factorial of a number r. If r is not a natural
* number, the gamma function as an extension to the factorial
* function is used.
*
*********************************************************************************/
globals
/*************************************************************************
* Customizable globals
*************************************************************************/
// Do you want the system to store primes that were once detected?
private constant boolean STORE_DETECTED_PRIMES = true
/*************************************************************************
* End of customizable globals
*************************************************************************/
public hashtable h
private constant real E_INV = 0.3678794
private constant real LOG_02_FACTOR = 1.4429504
private constant real LOG_10_FACTOR = 0.4342945
private constant real LN_FACTOR = 1.2840254
private constant real LN_FACTOR_INV = 0.7788008
endglobals
struct Math //extends array
// Constants
static constant real Pi = 3.141593
static constant real E = 2.718282
static constant real Phi = 1.618034
static constant real Inf = Pow(2.0, 128.0)
static constant integer MinInt = -2147483648
static constant integer MaxInt = 2147483647
// Absolute value
static method abs takes real r returns real
if r < 0 then
return -r
endif
return r
endmethod
// Signum
static method sig takes real r returns real
if r > 0 then
return 1.0
elseif r < 0 then
return -1.0
endif
return 0.0
endmethod
// Min-Max
static method max takes real r1, real r2 returns real
if r1 < r2 then
return r2
endif
return r1
endmethod
static method min takes real r1, real r2 returns real
if r1 < r2 then
return r1
endif
return r2
endmethod
// Modulus
static method mod takes real r1, real r2 returns real
local real modulus = r1 - I2R(R2I(r1/r2))*r2
if modulus < 0 then
set modulus = modulus + r2
endif
return modulus
endmethod
static method modInt takes integer n1, integer n2 returns integer
local integer modulus = n1 - (n1/n2)*n2
if modulus < 0 then
set modulus = modulus + n2
endif
return modulus
endmethod
static method multiMod takes integer n1, integer n2, integer mod returns integer
local integer factor1 = R2I(floor(n1/mod))
local integer factor2 = R2I(floor(n2/mod))
local integer modulus
if factor1 == 0 then
set factor1 = 1
endif
if factor2 == 0 then
set factor2 = 1
endif
if n1 > mod/2 and n2 > mod/2 then
set n1 = (n1 - factor1*mod)*(n2 - factor2*mod)
else
set n1 = n1*n2
endif
set n2 = mod
set modulus = n1 - (n1/n2)*n2
if modulus < 0 then
set modulus = modulus + n2
endif
return modulus
endmethod
static method expMod takes integer x, integer n, integer modulo returns integer
local string exponent = ""
local integer result = 1
local integer stringLen
local integer i = 0
loop
if modInt(n, 2) == 1 then
set exponent = "1"+exponent
else
set exponent = "0"+exponent
endif
set n = n/2
exitwhen n < 1
endloop
set stringLen = StringLength(exponent)
loop
exitwhen i >= stringLen
set result = multiMod(result, result, modulo)
if SubString(exponent, i, i + 1) == "1" then
set result = multiMod(result, x, modulo)
endif
set i = i + 1
endloop
return result
endmethod
// Digits
static method digits takes real r returns integer
local string s = R2S(r)
local integer i = 0
loop
exitwhen SubString(s, i, i + 1) == "."
set i = i + 1
endloop
if r < 0 then
return i - 1
endif
return i
endmethod
// Logarithms
static method ln takes real r returns real
local real sum = 0.0
local real sign = 1.0
debug if r < 0.0 then
debug call ThrowError(true, "Maths", "ln", "Math", 0, "Logarithm of negative number is undefined!")
debug endif
if r < 1.0 then
set r = 1.0/r
set sign = -1.0
endif
loop
exitwhen r < E
set r = r*E_INV
set sum = sum + 1.0
endloop
loop
exitwhen r < LN_FACTOR
set r = r*LN_FACTOR_INV
set sum = sum + 0.25
endloop
return sign*(sum + 0.125*(r - 1.0)*(1 + 9.0/(2.0 + r) + 4.5/(0.5 + r) + 1.0/r))
endmethod
static method log2 takes real r returns real
return LOG_02_FACTOR*ln(r)
endmethod
static method log10 takes real r returns real
return LOG_10_FACTOR*ln(r)
endmethod
static method log takes real base, real arg returns real
return ln(arg)/ln(base)
endmethod
// Hyperbolic functions
static method sinh takes real r returns real
return 0.5*(Pow(E, r) - Pow(E, -r))
endmethod
static method cosh takes real r returns real
return 0.5*(Pow(E, r) + Pow(E, -r))
endmethod
static method tanh takes real r returns real
return sinh(r)/cosh(r)
endmethod
static method asinh takes real r returns real
return ln(r + SquareRoot(r*r + 1))
endmethod
static method acosh takes real r returns real
return ln(r + SquareRoot(r*r - 1))
endmethod
static method atanh takes real r returns real
return 0.5*ln((1 + r)/(1 - r))
endmethod
// Rounding
static method floor takes real r returns real
if r < 0 then
return -I2R(R2I(-r))
endif
return I2R(R2I(r))
endmethod
static method ceil takes real r returns real
if floor(r) == r then
return r
elseif r < 0 then
return -(I2R(R2I(-r)) + 1.0)
endif
return I2R(R2I(r)) + 1.0
endmethod
static method round takes real r returns real
if r > 0 then
return I2R(R2I(r + 0.5))
endif
return I2R(R2I(r - 0.5))
endmethod
static method fractional takes real r returns real
return r - floor(r)
endmethod
static method mergeFloat takes real r returns real
local real afterC = fractional(r)
local real beforeC = floor(r)
local string beforeComma = R2S(beforeC)
local string afterComma = R2S(afterC)
local string subString
local integer i = 0
local integer stringLen = StringLength(beforeComma)
local integer endPosition = 0
if afterC == 0 then
return beforeC
endif
loop
exitwhen SubString(beforeComma, i, i + 1) == "."
set i = i + 1
endloop
set beforeComma = SubString(beforeComma, 0, i)
set i = StringLength(afterComma)
loop
set subString = SubString(afterComma, i, i + 1)
exitwhen subString == "."
if endPosition == 0 and subString != "0" and subString != "" then
set endPosition = i
endif
set i = i - 1
endloop
return S2R(beforeComma+SubString(afterComma, i + 1, endPosition + 1))
endmethod
// Type checks
static method isDigit takes string s returns boolean
return not (StringLength(s) != 1 or S2R(s) == 0 and s != "0")
endmethod
static method isInteger takes real r returns boolean
return I2R(R2I(r)) == r
endmethod
static method isEven takes real r returns boolean
return mod(r, 2.0) == 0
endmethod
static method isPrime takes integer n returns boolean
local integer s
local integer d
local integer a = 2
local integer temp
local integer counter
local integer dSave
local integer modulus
local boolean firstTest = false
local boolean secondTest = false
if n == 2 or n == 7 or n == 61 then
return true
elseif isEven(n) or n < 2 then
return false
endif
static if STORE_DETECTED_PRIMES then
if LoadBoolean(h, n, 0) then
return LoadBoolean(h, n, 1)
endif
endif
if n < 157 then
set a = n
loop
exitwhen a == 1
if modInt(n, a) == 0 and a != n then
static if STORE_DETECTED_PRIMES then
call SaveBoolean(h, n, 0, true)
call SaveBoolean(h, n, 1, false)
endif
return false
endif
set a = a - 1
endloop
static if STORE_DETECTED_PRIMES then
call SaveBoolean(h, n, 0, true)
call SaveBoolean(h, n, 1, true)
endif
return true
endif
set s = R2I(floor(log2(n - 1)))
loop
set temp = R2I(Pow(2, I2R(s)))
exitwhen modInt(n - 1, temp) == 0
set s = s - 1
endloop
set d = (n - 1)/(R2I(Pow(2, I2R(s))))
set dSave = d
set a = 2
set counter = 0
loop
exitwhen counter > s
set modulus = expMod(a, d, n)
if (counter == 0 and modulus == 1) or (counter > 0 and modulus - n == -1) then
set firstTest = true
exitwhen true
endif
set d = 2*d
set counter = counter + 1
if counter == 1 then
set d = dSave
endif
endloop
if not firstTest then
static if STORE_DETECTED_PRIMES then
call SaveBoolean(h, n, 0, true)
call SaveBoolean(h, n, 1, false)
endif
return false
endif
set a = 7
set d = dSave
set counter = 0
loop
exitwhen counter > s
set modulus = expMod(a, d, n)
if (counter == 0 and modulus == 1) or (counter > 0 and modulus - n == -1) then
if firstTest then
set secondTest = true
exitwhen true
endif
endif
set d = 2*d
set counter = counter + 1
if counter == 1 then
set d = dSave
endif
endloop
if not secondTest then
static if STORE_DETECTED_PRIMES then
call SaveBoolean(h, n, 0, true)
call SaveBoolean(h, n, 1, false)
endif
return false
endif
set a = 61
set d = dSave
set counter = 0
loop
exitwhen counter > s
set modulus = expMod(a, d, n)
if (counter == 0 and modulus == 1) or (counter > 0 and modulus - n == -1) then
if secondTest then
static if STORE_DETECTED_PRIMES then
call SaveBoolean(h, n, 0, true)
call SaveBoolean(h, n, 1, true)
endif
return true
endif
endif
set d = 2*d
set counter = counter + 1
if counter == 1 then
set d = dSave
endif
endloop
static if STORE_DETECTED_PRIMES then
call SaveBoolean(h, n, 0, true)
call SaveBoolean(h, n, 1, false)
endif
return false
endmethod
// Factorial
static method factorial takes real r returns real
local real z = 1.0
if floor(r) == r then
debug if r < 0 then
debug call ThrowError(true, "Maths", "factorial", "Math", 0, "Factorial of negative number is not defined!")
debug endif
if r == 0 then
return 1.0
endif
loop
exitwhen r == 0.0
set z = z*r
set r = r - 1.0
endloop
return z
endif
set r = r + 1.0
return SquareRoot((2.0*Pi)/(r))*Pow(((1.0/E)*(r + 1.0/(12.0*r - 1.0/(10.0*r)))), r)
endmethod
endstruct
private module Init
private static method onInit takes nothing returns nothing
set h = InitHashtable()
endmethod
endmodule
private struct Inits extends array
implement Init
endstruct
endlibraryMath struct (function list)
readonly static real PiRefer to this field for the number pi, the ratio of a circle's circumference to its diameter
readonly static real ERefer to this field for the number E, the base of the natural exponential function.
readonly static real PhiRefer to this field for the number Phi, the golden ratio.
readonly static real InfRefer to this field for 2^128, the biggest real number Wc3 can handle. You can use -Math.Inf to get the smallest real number.
readonly static integer MinIntRefer to this field for -2147483648, the smallest integer number that Wc3 can handle.
readonly static integer MaxIntRefer to this field for 2147483647, the biggest integer number that Wc3 can handle.
static method abs takes real r returns realComputes the absolute value of a number.
static method sig takes real r returns realExtracts the sign of a real number.
static method max takes real r1, real r2 returns realReturns the bigger of two values r1 and r2.
static method min takes real r1, real r2 returns realReturns the smaller of two values r1 and r2.
static method mod takes real r1, real r2 returns realComputes the rest of the division r1/r2.
static method modInt takes integer n1, integer n2 returns integerComputes the modulo of n1/n2.
static method multiMod takes integer n1, integer n2, integer mod returns integerComputes the modulo of n1*n2/mod. Use this to compute themodulo of very large numbers.
static method expMod takes integer x, integer n, integer modulo returns integerComputes the modulo of x^n/modulo. Use this to compute the modulo of extremly large numbers.
static method digits takes real r returns integerReturns the number of digits before the comma of a given real number.
static method isDigit takes string s returns booleanDetermines whether a string is a digit or not.
static method isInteger takes real r returns booleanDetermines whether a real is integer or not.
static method isEven takes real r returns booleanDetermines the parity of a real number.
static method isPrime takes real r returns booleanDetermines whether a number is a prime or not by using a deterministic version of the Miller-Rabin test. Works for values about ~100000.
static method sinh takes real r returns realComputes the hyperbolic sine of a real number.
static method cosh takes real r returns realComputes the hyperbolic cosine of a real number.
static method tanh takes real r returns realComputes the hyperbolic tangent of a real number.
static method asinh takes real r returns realComputes the inverse hyperbolic sine of a real number.
static method acosh takes real r returns realComputes the inverse hyperbolic cosine of a real number.
static method atanh takes real r returns realComputes the inverse hyperbolic tangent of a real number.
static method ln takes real r returns realComputes the natural logarithm to a number by using Newton-Cotes. Reaches extremly high accuracies very efficiently. This method is used to compute all other logarithms and inverse hyperbolic functions.
static method log2 takes real r returns realComputes the binary logarithm to a number.
static method log10 takes real r returns realComputes the common logarithm to a number.
static method log takes real r1, real r2 returns realComputes the logarithm of a number r2 to the base r1. If you want to compute the logarithm to the bases 2, 10 or E, you should use the specific functions as they are faster.
static method floor takes real r returns realRounds a number to the next smallest integer.
static method ceil takes real r returns realRounds a number to the next largest integer.
static method round takes real r returns realRounds a number to the nearest whole number.
static method fractional takes real r returns realComputes the fractional part of a number.
static method mergeFloat takes real r returns realMerges the fracional and the non fractional parts of a number together to an integer number.
static method factorial takes real r returns realComputes the factorial of a number r. If r is not a natural number, the gamma function as an extension to the factorial function is used.
3. Implementation and Available Extensions
To implement this system, just copy and paste the Math and the IngameCalculator triggers to your map. The only requirement is vJass, then you can use it right away, same applies for the available Extensions.
3.1. MathParser
This is one Extension to the Math library, a Math Parser library making it possible to dynamically evaluate mathematic expressions. This can be used to implement an ingame calculator to the game which makes ingame calculations very comfortable. This can be also useful for several things like: mathematic minigames or riddles, calculations during debugging or as a comfort function for maps that have a complex stat/skill system. Also maps with economy simulation parts could benefit from this. The math interpreter is based on standard Matlab conventions and supports the following symbols:
- Numbers with or without decimal point, e.g.: 3, 4.3, 55.2
- Arithmetic operators: +, -, *, /
- Power: ^
- Parenthesis: ( )
- Result memory (stores the last computed result): ans
- Clear screen: clc
The interpreter is designed to be very robust towards the different typing styles of mathematical expressions. So you can write for example 5*(1+2) or 5(1+2), the interpreter will automatically bring it into an understandable form. With the formatExpression method it is garantueed that the expression will also follow the standard conventions in terms of spacing and operator placement. Finally the interpreter is provided with various syntax and math error messages which will throw exceptions if the entered expression is invalid. These error messages can be optionally turned of in the system configuration. Enclosed is the Plug-In code:
JASS:
library MathParser /* v 1.1.0.0
**********************************************************************************
*
* MathParser
* ¯¯¯¯¯¯¯¯¯¯
* By looking_for_help aka eey
*
* This system provides methods for parsing mathematically string expressions,
* represented as strings. Also methods for formating string expressions are
* provided, making it possible to implement an ingame calculator to the game.
*
***********************************************************************************
*
* Requirements
* ¯¯¯¯¯¯¯¯¯¯¯¯
* */ uses Maths /* hiveworkshop.com/forums/spells-569/advanced-maths-ingame-calculator-234024/?prev=r%3D20%26page%3D5
*
***********************************************************************************
*
* Implementation
* ¯¯¯¯¯¯¯¯¯¯¯¯¯¯
* To use this system, you need the library Math. Once you implemented it, just
* copy this script to your trigger editor, then you can use it straight away. To
* see how the evaluation function works, compare the example IngameCalculator
* trigger for an example usage.
*
***********************************************************************************
*
* System API
* ¯¯¯¯¯¯¯¯¯¯
* readonly static real ans
* - Stores the last result of the evaluation method. Initialized as 0.
*
* static method calculate takes string expression returns real
* - Use this method to calculate a mathematic expression presented as
* a string. Allowed values are numbers, the decimal seperator, basic
* arithmetic operators like +, -, *, / and ^ as well as parenthesis.
* You can also put "ans" into the expression to refer to the last
* calculation result. Error messages on math and syntax errors will
* be displayed if specified so in the configurable globals. The
* syntax parsing strictly follows Matlab conventions.
*
* static method formatExpression takes string expression returns string
* - Use this method to format an user defined expression so that it
* looks nice. Compare the IngameCalculator trigger for an example
* usage.
*
*********************************************************************************/
globals
/*************************************************************************
* Customizable globals
*************************************************************************/
// Do you want the system to display error messages on math errors?
private constant boolean DISPLAY_MATH_ERRORS = true
// Do you want the system to display error messages on syntax errors?
private constant boolean DISPLAY_SYNTAX_ERRORS = true
/*************************************************************************
* End of customizable globals
*************************************************************************/
endglobals
private module Init
private static method onInit takes nothing returns nothing
call init()
endmethod
endmodule
struct MathParser extends array
readonly static real ans = 0.0
private static constant integer ADDITION = 1
private static constant integer SUBSTRACTION = 2
private static constant integer MULTIPLICATION = 3
private static constant integer DIVISION = 4
private static constant integer EXPONENTIATION = 5
private static method getPriority takes string op returns integer
return LoadInteger(Maths_h, StringHash(op), 0)
endmethod
private static method error takes string s, integer flag returns nothing
local real crashThread
if flag == 0 then
static if DISPLAY_MATH_ERRORS then
call DisplayTimedTextToPlayer(GetLocalPlayer(), 0.0, 0.0, 60.0, "|cffff0000Math Error!|r "+s)
endif
else
static if DISPLAY_SYNTAX_ERRORS then
call DisplayTimedTextToPlayer(GetLocalPlayer(), 0.0, 0.0, 60.0, "|cffff0000Syntax Error!|r "+s)
endif
endif
set crashThread = 0/0
endmethod
private static method convertExpression takes string expression returns string
local integer stringLen = StringLength(expression)
local integer i = 0
local integer stackCounter = -1
local string postfix = ""
local string array stack
local string actualChar
local string prevChar
local boolean decimalDetected = false
local boolean numberDetected = false
local boolean numberOnceDetected = false
local boolean unaryOperator = false
local integer openBraces = 0
loop
exitwhen i > stringLen
set prevChar = SubString(expression, i - 1, i)
set actualChar = SubString(expression, i, i + 1)
set unaryOperator = not (prevChar == ")" or Math.isDigit(prevChar))
if actualChar == ")" and openBraces < 1 then
call thistype.error("Unbalanced parenthesis!", 1)
endif
if actualChar == "m" or actualChar == "p" or actualChar == "M" or actualChar == "P" then
call thistype.error("Undefined symbols used!", 1)
endif
if actualChar == "+" and unaryOperator and prevChar != "^" then
set actualChar = "p"
elseif actualChar == "-" and unaryOperator and prevChar != "^" then
set actualChar = "m"
elseif actualChar == "-" and unaryOperator and prevChar == "^" then
set actualChar = "M"
elseif actualChar == "+" and unaryOperator and prevChar == "^" then
set actualChar = "P"
endif
if Math.isDigit(actualChar) then
set postfix = postfix+actualChar
set numberDetected = true
set numberOnceDetected = true
elseif actualChar == "." then
if decimalDetected == false and Math.isDigit(SubString(expression, i - 1, i)) and Math.isDigit(SubString(expression, i + 1, i + 2)) then
set postfix = postfix+actualChar
set decimalDetected = true
else
call thistype.error("Incorrect use of decimal point!", 1)
endif
elseif thistype.isOperator(actualChar) or actualChar == "(" or actualChar == ")" then
set decimalDetected = false
if numberDetected then
set numberDetected = false
set postfix = postfix+" "
endif
if thistype.getPriority(actualChar) > thistype.getPriority(stack[stackCounter]) or actualChar == "(" then
set stackCounter = stackCounter + 1
set stack[stackCounter] = actualChar
if actualChar == "(" then
set openBraces = openBraces + 1
endif
elseif openBraces > 0 and actualChar != ")" and actualChar != "(" and thistype.getPriority(actualChar) <= thistype.getPriority(stack[stackCounter]) then
loop
exitwhen stack[stackCounter] == "("
set postfix = postfix+stack[stackCounter]+" "
set stackCounter = stackCounter - 1
endloop
set stackCounter = stackCounter + 1
set stack[stackCounter] = actualChar
else
if actualChar == ")" then
set openBraces = openBraces - 1
loop
exitwhen stack[stackCounter] == "("
set postfix = postfix+stack[stackCounter]+" "
set stackCounter = stackCounter - 1
endloop
set stack[stackCounter] = ""
set stackCounter = stackCounter - 1
else
loop
exitwhen stackCounter < 0
set postfix = postfix+stack[stackCounter]+" "
set stackCounter = stackCounter - 1
endloop
set stackCounter = stackCounter + 1
set stack[stackCounter] = actualChar
endif
endif
else
if i != stringLen then
call thistype.error("Undefined symbols used!", 1)
endif
endif
set i = i + 1
endloop
if not numberOnceDetected then
call thistype.error("Invalid expression!", 1)
endif
if stackCounter >= 0 then
if openBraces > 0 then
call thistype.error("Unbalanced parenthesis!", 1)
endif
loop
exitwhen stackCounter < 0
if stack[stackCounter] != "(" then
if numberDetected then
set postfix = postfix+" "+stack[stackCounter]+" "
set numberDetected = false
else
set postfix = postfix+stack[stackCounter]+" "
endif
endif
set stackCounter = stackCounter - 1
endloop
endif
set stringLen = StringLength(postfix)
if Math.isDigit(SubString(postfix, stringLen - 1, stringLen)) then
set postfix = postfix+" "
endif
return postfix
endmethod
private static method subCalc takes string op1, string op2, string op returns real
local real r1 = S2R(op1)
local real r2 = S2R(op2)
local integer localOp
if op1 == null or op2 == null then
call thistype.error("Unbalanced operators!", 1)
endif
set localOp = LoadInteger(Maths_h, StringHash(op), 1)
if localOp < MULTIPLICATION then
if localOp == ADDITION then
return r1 + r2
else
return r1 - r2
endif
else
if localOp == MULTIPLICATION then
return r1*r2
elseif localOp == DIVISION then
if r2 == 0 then
call thistype.error("Division by zero!", 0)
endif
return r1/r2
else
if r1 < 0.0 and not Math.isInteger(r2) then
call thistype.error("(N-th) square root from negativ value not defined!", 0)
endif
return Pow(r1, r2)
endif
endif
call thistype.error("Undefined operators!", 1)
return 0.0
endmethod
private static method isOperator takes string s returns boolean
return s == "+" or s == "-" or s == "*" or s == "/" or s == "^" or s == "(" or s == "p" or s == "m" or s == "P" or s == "M"
endmethod
private static method prepareExpression takes string expression returns string
local integer stringLen = StringLength(expression)
local integer i = 0
local string actualChar
local string prevChar
local string nextChar
loop
exitwhen i > stringLen
set actualChar = SubString(expression, i, i + 1)
if actualChar == " " then
set expression = SubString(expression, 0, i)+SubString(expression, i + 1, stringLen)
set i = i - 1
endif
set i = i + 1
endloop
set i = 0
set stringLen = StringLength(expression)
loop
exitwhen i > stringLen
if SubString(expression, i, i + 3) == "ans" then
set expression = SubString(expression, 0, i)+"("+R2S(ans)+")"+SubString(expression, i + 3, stringLen)
set stringLen = StringLength(expression)
endif
set prevChar = SubString(expression, i - 1, i)
set actualChar = SubString(expression, i, i + 1)
set nextChar = SubString(expression, i + 1, i + 2)
if actualChar == "+" then
if SubString(expression, i + 1, i + 2) == "+" then
if Math.isDigit(SubString(expression, i - 1, i)) then
set expression = SubString(expression, 0, i)+"+"+SubString(expression, i + 2, stringLen)
else
set expression = SubString(expression, 0, i)+SubString(expression, i + 2, stringLen)
endif
set i = i - 1
elseif SubString(expression, i + 1, i + 2) == "-" then
set expression = SubString(expression, 0, i)+"-"+SubString(expression, i + 2, stringLen)
set i = i - 1
endif
elseif actualChar == "-" then
if SubString(expression, i + 1, i + 2) == "+" then
set expression = SubString(expression, 0, i)+"-"+SubString(expression, i + 2, stringLen)
set i = i - 1
elseif SubString(expression, i + 1, i + 2) == "-" then
if Math.isDigit(SubString(expression, i - 1, i)) then
set expression = SubString(expression, 0, i)+"+"+SubString(expression, i + 2, stringLen)
else
set expression = SubString(expression, 0, i)+SubString(expression, i + 2, stringLen)
endif
set i = i - 1
endif
elseif actualChar == "(" and (Math.isDigit(prevChar) or prevChar == ")") then
set expression = SubString(expression, 0, i)+"*"+SubString(expression, i, stringLen)
set stringLen = StringLength(expression)
set i = i - 1
elseif actualChar == ")" and Math.isDigit(nextChar) then
set expression = SubString(expression, 0, i + 1)+"*"+SubString(expression, i + 1, stringLen)
set stringLen = StringLength(expression)
set i = i - 1
endif
set i = i + 1
endloop
return expression
endmethod
private static method evaluateExpression takes string postfix returns real
local integer stringLen = StringLength(postfix)
local integer i = 0
local integer position = 0
local integer counter = 0
local integer stackCounter = -1
local string actualToken
local string array stack
local real result = 0.0
loop
exitwhen i == stringLen
if SubString(postfix, i, i + 1) == " " then
set actualToken = SubString(postfix, position, position + counter)
if Math.isDigit(SubString(actualToken, 0, 1)) then
set stackCounter = stackCounter + 1
set stack[stackCounter] = actualToken
else
if not (actualToken == "m " or actualToken == "p " or actualToken == "M " or actualToken == "P ") then
set result = thistype.subCalc(stack[stackCounter - 1], stack[stackCounter], actualToken)
set stack[stackCounter] = ""
set stack[stackCounter - 1] = R2S(result)
set stackCounter = stackCounter - 1
else
if actualToken == "m " or actualToken == "M " then
if S2R(stack[stackCounter]) > 0 then
set stack[stackCounter] = "-"+stack[stackCounter]
else
set stack[stackCounter] = SubString(stack[stackCounter], 1, StringLength(stack[stackCounter]))
endif
endif
endif
endif
set position = i + 1
set counter = 0
endif
set i = i + 1
set counter = counter + 1
endloop
return S2R(stack[0])
endmethod
static method calculate takes string expression returns real
set ans = thistype.evaluateExpression(thistype.convertExpression(thistype.prepareExpression(expression)))
return ans
endmethod
static method formatExpression takes string expression returns string
local integer i = 0
local integer stringLen = StringLength(expression)
local string prevChar
local string nextChar
local string actualChar
local string prevAnsToken
local string nextAnsToken
local boolean unaryOperator = false
loop
exitwhen i > stringLen
if SubString(expression, i, i + 1) == " " then
set expression = SubString(expression, 0, i)+SubString(expression, i + 1, stringLen)
set i = i - 1
endif
set i = i + 1
endloop
set i = 0
set stringLen = StringLength(expression)
loop
exitwhen i > stringLen
set actualChar = SubString(expression, i, i + 1)
if actualChar == "+" then
if SubString(expression, i + 1, i + 2) == "+" then
if Math.isDigit(SubString(expression, i - 1, i)) then
set expression = SubString(expression, 0, i)+"+"+SubString(expression, i + 2, stringLen)
else
set expression = SubString(expression, 0, i)+SubString(expression, i + 2, stringLen)
endif
set i = i - 1
elseif SubString(expression, i + 1, i + 2) == "-" then
set expression = SubString(expression, 0, i)+"-"+SubString(expression, i + 2, stringLen)
set i = i - 1
endif
elseif actualChar == "-" then
if SubString(expression, i + 1, i + 2) == "+" then
set expression = SubString(expression, 0, i)+"-"+SubString(expression, i + 2, stringLen)
set i = i - 1
elseif SubString(expression, i + 1, i + 2) == "-" then
if Math.isDigit(SubString(expression, i - 1, i)) then
set expression = SubString(expression, 0, i)+"+"+SubString(expression, i + 2, stringLen)
else
set expression = SubString(expression, 0, i)+SubString(expression, i + 2, stringLen)
endif
set i = i - 1
endif
endif
set i = i + 1
endloop
set i = 0
set stringLen = StringLength(expression)
loop
exitwhen i > stringLen
set actualChar = SubString(expression, i, i + 1)
set prevChar = SubString(expression, i - 1, i)
set nextChar = SubString(expression, i + 1, i + 2)
set prevAnsToken = SubString(expression, i - 3, i)
set nextAnsToken = SubString(expression, i + 1, i + 4)
set unaryOperator = not (prevChar == ")" or Math.isDigit(prevChar) or prevAnsToken == "ans")
if actualChar == "+" and not unaryOperator then
set expression = SubString(expression, 0, i)+" + "+SubString(expression, i + 1, stringLen)
set stringLen = StringLength(expression)
set i = i + 1
elseif actualChar == "+" and unaryOperator then
set expression = SubString(expression, 0, i)+SubString(expression, i + 1, stringLen)
set stringLen = StringLength(expression)
set i = i - 1
elseif actualChar == "-" and not unaryOperator then
set expression = SubString(expression, 0, i)+" - "+SubString(expression, i + 1, stringLen)
set stringLen = StringLength(expression)
set i = i + 1
elseif actualChar == "(" and (Math.isDigit(prevChar) or prevChar == ")") then
set expression = SubString(expression, 0, i)+"*"+SubString(expression, i, stringLen)
set stringLen = StringLength(expression)
set i = i - 1
elseif actualChar == ")" and Math.isDigit(nextChar) then
set expression = SubString(expression, 0, i + 1)+"*"+SubString(expression, i + 1, stringLen)
set stringLen = StringLength(expression)
set i = i - 1
endif
if prevAnsToken == "ans" and (Math.isDigit(actualChar) or actualChar == "(" or SubString(expression, i, i + 3) == "ans") then
set expression = SubString(expression, 0, i)+"*"+SubString(expression, i, stringLen)
set stringLen = StringLength(expression)
set i = i - 1
elseif nextAnsToken == "ans" and (Math.isDigit(actualChar) or actualChar == ")") then
set expression = SubString(expression, 0, i + 1)+"*"+SubString(expression, i + 1, stringLen)
set stringLen = StringLength(expression)
set i = i - 1
endif
set i = i + 1
endloop
return expression
endmethod
private static method init takes nothing returns nothing
call SaveInteger(Maths_h, StringHash("+"), 0, 1)
call SaveInteger(Maths_h, StringHash("-"), 0, 1)
call SaveInteger(Maths_h, StringHash("*"), 0, 2)
call SaveInteger(Maths_h, StringHash("/"), 0, 2)
call SaveInteger(Maths_h, StringHash("m"), 0, 3)
call SaveInteger(Maths_h, StringHash("p"), 0, 3)
call SaveInteger(Maths_h, StringHash("^"), 0, 4)
call SaveInteger(Maths_h, StringHash("M"), 0, 5)
call SaveInteger(Maths_h, StringHash("P"), 0, 5)
call SaveInteger(Maths_h, StringHash("("), 0, 6)
call SaveInteger(Maths_h, StringHash("+ "), 1, ADDITION)
call SaveInteger(Maths_h, StringHash("- "), 1, SUBSTRACTION)
call SaveInteger(Maths_h, StringHash("* "), 1, MULTIPLICATION)
call SaveInteger(Maths_h, StringHash("/ "), 1, DIVISION)
call SaveInteger(Maths_h, StringHash("^ "), 1, EXPONENTIATION)
endmethod
implement Init
endstruct
endlibrary
JASS:
library IngameCalculator uses MathParser
globals
/*************************************************************************
* Customizable globals
*************************************************************************/
// Define a command before performing a calculation, e.g. "-calc ".
// Use an empty string for no command.
private constant string commandString = ""
// Type in this string to clear the screen.
private constant string clearScreen = "clc"
/*************************************************************************
* End of customizable globals
*************************************************************************/
endglobals
private struct Calculator extends array
readonly static string expression
private static method onEnter takes nothing returns nothing
set expression = GetEventPlayerChatString()
if SubString(expression, 0, StringLength(commandString)) == commandString then
set expression = SubString(expression, StringLength(commandString), StringLength(expression))
if expression == clearScreen then
call ClearTextMessages()
else
call DisplayTimedTextToPlayer(GetLocalPlayer(), 0.0, 0.0, 60.0, MathParser.formatExpression(expression)+" = "+R2S(MathParser.calculate(expression)))
endif
endif
endmethod
implement CalcInit
endstruct
module CalcInit
private static method onInit takes nothing returns nothing
local trigger t = CreateTrigger()
local code c = function thistype.onEnter
local integer i = 0
loop
exitwhen i > 11
call TriggerRegisterPlayerChatEvent(t, Player(i), "", false)
set i = i + 1
endloop
call TriggerAddCondition(t, Filter(c))
set t = null
set c = null
endmethod
endmodule
endlibraryMathParser struct
readonly static real ansStores the last result of the evaluation method. Initialized as 0.
static method calculate takes string expression returns realUse this method to calculate a mathematic expression presented as a string. Allowed values are numbers, the decimal seperator, basic arithmetic operators like +, -, *, / and ^ as well as parenthesis. You can also put "ans" into the expression to refer to the last calculation result. Error messages on math and syntax errors will be displayed if specified so in the configurable globals. The syntax parsing strictly follows Matlab conventions.
static method formatExpression takes string expression returns stringUse this method to format an user defined expression so that it looks nice. Compare the IngameCalculator trigger for an example usage.
3.2. Matrices
This is another Extension to the basic Maths library which gives you the possiblity to perform Matrix operations in Warcraft 3. Matrices can basically be used like 2D-Arrays with this library. The library also provides advanced methods to initialize, reshape or to perform calculations with Matrices. Gaußian Eliminiation with pivotising is implemented as well as solving a System of Linear Equations (SLE), inverting or transposing a Matrix as well as calculating the norm, condition or trace.
This library will serve as a base for more advanced libraries in the future which allow curve fitting, trajectory interpolation and many more.
JASS:
library Matrices /* v 1.1.0.1
**********************************************************************************
*
* Matrices
* ¯¯¯¯¯¯¯¯
* By looking_for_help aka eey
*
* This system provides advanced methods for handling Matrices in Warcraft 3.
* Features like Matrix multiplication, calculation of norms or trace as well as
* solving a system of linear equations with Gauss-Elimination are implemented.
* The system also provides a big variety of functions to initialize, copy or
* reshape Matrices.
*
* Credits go to Magtheridon for helping with the Systems API.
*
**********************************************************************************
*
* Requirements
* ¯¯¯¯¯¯¯¯¯¯¯¯
* */ uses Maths /* hiveworkshop.com/forums/spells-569/advanced-maths-ingame-calculator-234024/?prev=r%3D20%26page%3D5
*
**********************************************************************************
*
* Implementation
* ¯¯¯¯¯¯¯¯¯¯¯¯¯¯
* To use this system just copy it into an empty trigger in your map. As this
* system uses the Math library you should install it first to get the system
* to work. The Math library can be found under the link above.
*
**********************************************************************************
*
* System API
* ¯¯¯¯¯¯¯¯¯¯
*
* Struct usage
* -----------------------------
*
* struct Matrix
* - This struct provides the methods and logic to use Matrices in
* Warcraft 3 with this system. Use the create method to allocate a
* new instance of a Matrix of your desired size. The Matrix can then
* be used like a 2D-Array (example displayed above) and provides
* various methods to perform advanced Matrix operations.
*
* 0 1 2
* 0 [0][0][0]
* local Matrix mat = Matrix.create(3, 3) = 1 [0][0][0]
* 2 [0][0][0]
*
*
* Operators
* -----------------------------
*
* [] operators
* - Use the [] operators to access directly to the values of a given
* Matrix. For example mat[2][1] will return the element in the third
* row, second column. Note that the indices are, like Wc3 arrays,
* zero-based.
*
*
* Fields
* -----------------------------
*
* readonly integer n
* - Specifies the number of rows of a given Matrix.
*
* readonly integer m
* - Specifies the number of columns of a given Matrix.
*
* readonly static Matrix Invalid_Matrix
* - An invalid Matrix of the size 0 x 0. You can't create such a Matrix,
* so if you need one, use this field. Some algorithms, such as solveSLE
* return such a Matrix if no solution for a given System of Linear
* Equations could be found. You can use the method isValid() to
* determine wether a Matrix is valid or not.
*
* static constant integer ONE_NORM
* - Use this as a parameter for the norm method to specify that the method
* should calculate the one norm (maximum of column sum absolute values).
*
* static constant integer EUCLIDEAN_NORM
* - Use this as a parameter for the norm method to specify that the method
* should calculate the euclidean norm (square root of sum of squares).
*
* static constant integer INFINITY_NORM
* - Use this as a parameter for the norm method to specify that the method
* should calculate the infinity norm (maximum of row sum absolute values).
*
* static constant integer METHOD_ROW_WISE
* - Use this as a parameter for methods like initStepWise or reShape to
* specify whether the method should be applied row-wise.
*
* static constant integer METHOD_COL_WISE
* - Use this as a parameter for methods like initStepWise or reShape to
* specify whether the method should be applied col-wise.
*
*
* Methods
* -----------------------------
*
* static method create takes integer nDim, integer mDim returns Matrix
* - Creates a new n x m Matrix with the maximum size of MAX_MATRIX_SIZE
* (specified in the globals block). The Matrix is initialized with
* zeros.
*
* method destroy takes nothing returns nothing
* - Destroys a given Matrix to free its memory usage.
*
* method display takes nothing returns nothing
* - Use this method to display a Matrix ingame. This is especially
* meant for debugging issues.
*
* method isValid takes nothing returns boolean
* - Checks whether a given Matrix is valid (means: not empty) or not.
*
* method isEqual takes Matrix mat returns boolean
* - Checks whether two Matrices are equal or not. If A == B then
* A.isEqual(B) returns true.
*
* method init takes real value returns nothing
* - Use this method to initialize a Matrix with a desired real value.
* Note that this method does not create a new instance of the Matrix
* object, as well as all methods that only initialize the values of a
* Matrix.
*
* method eye takes nothing returns nothing
* - Use this method to initialize an Identity Matrix.
*
* method diag takes real value, integer whichDiagonal returns nothing
* - Use this method to initialize a Diagonal Matrix with a desired real
* value. Use the second argument to specify which diagonal you want
* to set (zero is the main diagonal, negative values address the
* upper, positive values the lower diagonals).
*
* method rand takes real lowerBound, real upperBound returns nothing
* - Use this method to initialize a Matrix with random real values.
*
* method initStepWise takes real startValue, real steps returns nothing
* - Use this method to initialize a matrix from a given start value in
* ascending or descending order specified by the steps parameter.
*
* method assign takes nothing returns Matrix
* - Use this method to assign a Matrix to another Matrix. For example
* set B = A.assign() will copy A to B. Note that A and B must be of
* equal size for this operation to work.
*
* method addScalar takes real value returns Matrix
* - This method performs a element-wise addition of a given real value
* and returns the new Matrix. Example: A.addScalar(2.0) will add the
* value 2.0 to all elements of the Matrix A.
*
* method subScalar takes real value returns Matrix
* - This method performs a element-wise subtraction of a given real
* value.
*
* method mulScalar takes real value returns Matrix
* - This method performs a element-wise multiplication by a given real
* value.
*
* method divScalar takes real value returns Matrix
* - This method performs a element-wise division by a given real value.
*
* method abs takes nothing returns Matrix
* - This method performs the abs function on all Matrix elements.
*
* method add takes Matrix whichMatrix returns Matrix
* - Matrix addition. The expression A.add(B) where both A and B are
* Matrices returns the resulting Matrix A + B. Note that the Matrices
* must follow common Matrix calculation rules, like here that A and B
* have the same size.
*
* method sub takes Matrix whichMatrix returns MAtrix
* - Matrix substraction. Same as the add method, A.sub(B) performs
* A - B.
*
* method multiply takes Matrix whichMatrix returns Matrix
* - Matrix multiplication. The expression A.multiply(B) performs the
* operation A*B. Note that A's number of columns must equal B's
* number of rows for this operation to be well-defined.
*
* method transpose takes nothing returns Matrix
* - Matrix transposition. The expression A.transpose() computes A^T.
*
* method invert takes nothing returns Matrix
* - Matrix inversion. Use A.invert() to calculate A^-1, the inverse
* of the Matrix A. Be aware of the fact that not every Matrix is
* invertable.
*
* method gauss takes nothing returns Matrix
* - Use this method to perform a Gauss-Elimination with pivotising.
* The result is a upper triangular Matrix.
*
* method solveSLE takes Matrix b returns Matrix
* - Use this method to solve a System of Linear Equations following
* the common notation A*x = b. To calculate x use A.solveSLE(b)
* where A is the system Matrix and b is the solution vector. If the
* SLE has no unique solution, an invalid vector of size 0 x 0 is
* returned.
*
* method dotProduct takes Matrix b returns real
* - Use this method to calculate the dot product of two Vectors. Use
* it like a.dotProduct(b), which results in a^T*b. Calling this
* method is faster than performing the transposition manualy and
* should therefore be used if possible. To check whether two Vectors
* are orthogonal, the dot product must be zero.
*
* method crossProduct takes Matrix b returns Matrix
* - Use this method to calculate the cross product of two Vectors.
* This implementation only supports calculation of cross products
* for Vectors in R^3.
*
* method trace takes nothing returns real
* - Returns the trace of a given Matrix. Which is defined as the sum
* over its diagonal elements.
*
* method det takes nothing returns real
* - Returns the determinant of a given Matrix. From A.det() == 0
* follows for example that A is not invertable.
*
* method rank takes nothing returns integer
* - Returns the rank of a given Matrix. A square Matrix must have full
* rank to be invertable, which means that A.rank() == A.n must return
* true.
*
* method norm takes integer whichNorm returns real
* - Computes the norm of a given Matrix. You can choose between different
* norms by using the constants defined in the Matrix struct. Valid
* values for the whichNorm parameter are ONE_NORM, EUCLIDEAN_NORM
* and the INFINITY_NORM.
*
* method cond takes integer whichNorm returns real
* - Computes the condition of a Matrix. You can specify which Norm you
* want to use for that purpose by the parameter whichNorm (see method
* norm). Note that the Matrix must be invertable otherwise the
* condition will be infinity.
*
* method subMatrix takes integer startRow, integer startCol, integer endRow,
* integer endCol returns Matrix
* - This method can be used to get a sub Matrix out of another Matrix.
* With the parameters startRow and startCol you can specify where
* the submatrix should begin and the parameters endRow as well as
* endCol define where to end the sub Matrix. If A is for example
* a 3 x 3 Matrix, A.subMatrix(0, 0, 2, 0) will return the first
* column Vector of A, while A.subMatrix(0, 0, 1, 1) will return
* the first 2 x 2 sub Matrix of A and so on.
*
* method embed takes Matrix subMat, integer startRow, integer startCol
* returns Matrix
* - This method embeds one Matrix into another. If you have for example
* the 3 x 3 Matrix A and the 2 x 2 Matrix B then A.embed(B, 0, 0)
* will assign the upper left sub matrix of A to the values of B. The
* parameters startRow and startCol specify where the embeding should
* start. Of course the sub matrix must fit into the Matrix you want to
* embed it into, otherwise an error will be thrown.
*
* method concatH takes Matrix mat returns Matrix
* - Use this method to concatenate two Matrices. The Matrices must
* have the same amount of rows for this operation to work. The Matrices
* will get concatenated horizontal, resulting for two n x m
* Matrices in a n x 2*m Matrix. Example: A.concatH(B) will concate-
* nate A to B (from the left side).
*
* method concatV takes Matrix mat returns Matrix
* - Use this method to concatenate two Matrices. The Matrices must
* have the same amount of columns for this operation to work. The
* Matrices will get concatenated vertically, resulting for two n x m
* Matrices in a 2*n x m Matrix. Example: A.concatV(B) will stack
* the Matrix B on A.
*
* method reShape takes integer newN, integer newM, integer whichMethod
* returns Matrix
* - Use this method to reshape a Matrix. If you have for example a
* 3 x 2 Matrix A, by performing A.reShape(2, 3, METHOD_ROW_WISE)
* the Matrix will get a 2 x 3 Matrix. The third parameter whichMethod
* determines whether the operation should be done row-wise or
* column-wise. METHOD_ROW_WISE and METHOD_COL_WISE are valid
* parameters. This can also be used to make a Vektor of a Matrix
* (or vice versa): A.reShape(6, 1, METHOD_COL_WISE) will stack
* all column Vektors of A to one 6 x 1 Vektor.
*
* method switchRow takes integer whichRow, integer newRow returns Matrix
* - Use this method to switch two different rows of a Matrix. The
* expression A.switchRow(0, 2) will switch the first with the third
* row. Note that both parameters whichRow and newRow must not exceed
* Matrix dimensions.
*
* method switchCol takes integer whichCol, integer newCol returns Matrix
* - Use this method to switch two different columns of a Matrix. Same
* rules as for switchRow apply here.
*
*********************************************************************************/
globals
/*************************************************************************
* Configurable globals
*************************************************************************/
// Accuracy for considering a Matrix too close to singularity
private constant real EPSILON = 0.01
// Do you want the system to display debug error messages?
private constant boolean DISPLAY_MATRIX_ERRORS = true
// Biggest possible n x n-Matrix
private constant integer MAX_MATRIX_SIZE = 50
/*************************************************************************
* End of configurable globals
*************************************************************************/
endglobals
private struct MatrixRow
real array values[MAX_MATRIX_SIZE]
integer maxCols
method operator [] takes integer column returns real
return this.values[column]
endmethod
method operator []= takes integer column, real value returns nothing
debug if column < 0 or column >= maxCols then
debug call ThrowError(true, "Matrices", "[]=", "MatrixRow", this, "Can't access Matrix! Index exceeds Matrix dimensions!")
debug endif
set this.values[column] = value
endmethod
static method create takes integer cols returns thistype
local thistype this = MatrixRow.allocate()
set this.maxCols = cols
return this
endmethod
endstruct
private module Inits
private static method onInit takes nothing returns nothing
set Matrix.Invalid_Matrix = Matrix.createInvalid()
endmethod
endmodule
struct Matrix
private MatrixRow array matRow[MAX_MATRIX_SIZE]
static constant integer ONE_NORM = 1
static constant integer EUCLIDEAN_NORM = 2
static constant integer INFINITY_NORM = 3
static constant integer METHOD_ROW_WISE = 0
static constant integer METHOD_COL_WISE = 1
readonly static Matrix Invalid_Matrix
readonly integer n
readonly integer m
method operator [] takes integer row returns MatrixRow
debug if row < 0 or row >= n then
debug call ThrowError(true, "Matrices", "[]", "Matrix", this, "Can't access Matrix! Index exceeds Matrix dimensions!")
debug endif
return this.matRow[row]
endmethod
static method create takes integer nDim, integer mDim returns thistype
local integer i = 0
local thistype this
if nDim < 1 or mDim < 1 then
debug call ThrowError(true, "Matrices", "create", "Matrix", 0, "Invalid Matrix!")
endif
set this = Matrix.allocate()
loop
exitwhen i > nDim - 1
set this.matRow[i] = MatrixRow.create(mDim)
set i = i + 1
endloop
set this.n = nDim
set this.m = mDim
return this
endmethod
private static method createInvalid takes nothing returns thistype
local thistype this = Matrix.allocate()
set this.n = 0
set this.m = 0
return this
endmethod
method isValid takes nothing returns boolean
return this.n == 0
endmethod
method isEqual takes Matrix mat returns boolean
local integer i = 0
local integer j = 0
if this.n != mat.n or this.m != mat.m then
return false
endif
loop
exitwhen i >= n
loop
exitwhen j >= m
if this.matRow[i][j] != mat[i][j] then
return false
endif
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return true
endmethod
method addScalar takes real value returns Matrix
local integer i = 0
local integer j = 0
local Matrix mat
debug if n < 1 then
debug call ThrowError(true, "Matrices", "addScalar", "Matrix", this, "Invalid Matrix!")
debug endif
set mat = Matrix.create(n, m)
loop
exitwhen i >= n
loop
exitwhen j >= m
set mat[i][j] = this.matRow[i][j] + value
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return mat
endmethod
method subScalar takes real value returns Matrix
local integer i = 0
local integer j = 0
local Matrix mat
debug if n < 1 then
debug call ThrowError(true, "Matrices", "subScalar", "Matrix", this, "Invalid Matrix!")
debug endif
set mat = Matrix.create(n, m)
loop
exitwhen i >= n
loop
exitwhen j >= m
set mat[i][j] = this.matRow[i][j] - value
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return mat
endmethod
method multScalar takes real value returns Matrix
local integer i = 0
local integer j = 0
local Matrix mat
debug if n < 1 then
debug call ThrowError(true, "Matrices", "multScalar", "Matrix", this, "Invalid Matrix!")
debug endif
set mat = Matrix.create(n, m)
loop
exitwhen i >= n
loop
exitwhen j >= m
set mat[i][j] = this.matRow[i][j]*value
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return mat
endmethod
method divScalar takes real value returns Matrix
local integer i = 0
local integer j = 0
local Matrix mat
debug if n < 1 then
debug call ThrowError(true, "Matrices", "divScalar", "Matrix", this, "Invalid Matrix!")
debug endif
set mat = Matrix.create(n, m)
loop
exitwhen i >= n
loop
exitwhen j >= m
set mat[i][j] = this.matRow[i][j]/value
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return mat
endmethod
method abs takes nothing returns Matrix
local integer i = 0
local integer j = 0
local Matrix mat
debug if n < 1 then
debug call ThrowError(true, "Matrices", "abs", "Matrix", this, "Invalid Matrix!")
debug endif
set mat = Matrix.create(n, m)
loop
exitwhen i >= n
loop
exitwhen j >= m
if this.matRow[i][j] >= 0 then
set mat[i][j] = this.matRow[i][j]
else
set mat[i][j] = -this.matRow[i][j]
endif
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return mat
endmethod
method eye takes real value returns nothing
local integer i = 0
local integer j = 0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "eye", "Matrix", this, "Invalid Matrix!")
debug endif
loop
exitwhen j >= n
loop
exitwhen i >= m
if i != j then
set this.matRow[j][i] = 0.0
else
set this.matRow[j][i] = 1.0
endif
set i = i + 1
endloop
set i = 0
set j = j + 1
endloop
endmethod
method diag takes real value, integer whichDiagonal returns nothing
local integer i = 0
local integer j = 0
local integer minDim
debug if n < 1 then
debug call ThrowError(true, "Matrices", "diag", "Matrix", this, "Invalid Matrix!")
debug endif
if n <= m then
set minDim = n - 1
else
set minDim = m - 1
endif
debug if whichDiagonal > minDim then
debug call ThrowError(true, "Matrices", "diag", "Matrix", this, "Diagonal Index exceeds Matrix dimensions!")
debug endif
loop
exitwhen j >= n
loop
exitwhen i >= m
if i != j - whichDiagonal then
set this.matRow[j][i] = 0.0
else
set this.matRow[j][i] = value
endif
set i = i + 1
endloop
set i = 0
set j = j + 1
endloop
endmethod
method init takes real value returns nothing
local integer i = 0
local integer j = 0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "init", "Matrix", this, "Invalid Matrix!")
debug endif
loop
exitwhen j >= n
loop
exitwhen i >= m
set this.matRow[j][i] = value
set i = i + 1
endloop
set i = 0
set j = j + 1
endloop
endmethod
method rand takes real lowerBound, real upperBound returns nothing
local integer i = 0
local integer j = 0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "rand", "Matrix", this, "Invalid Matrix!")
debug endif
loop
exitwhen j >= n
loop
exitwhen i >= m
set this.matRow[j][i] = GetRandomReal(lowerBound, upperBound)
set i = i + 1
endloop
set i = 0
set j = j + 1
endloop
endmethod
method initStepWise takes real startValue, real step, integer whichMethod returns nothing
local integer i = 0
local integer j = 0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "initStepWise", "Matrix", this, "Invalid Matrix!")
debug endif
debug if (whichMethod != METHOD_ROW_WISE and whichMethod != METHOD_COL_WISE) then
debug call ThrowError(true, "Matrices", "initStepWise", "Matrix", this, "Invalid method for initializing!")
debug endif
if whichMethod == METHOD_ROW_WISE then
loop
exitwhen j >= n
loop
exitwhen i >= m
set this.matRow[j][i] = startValue
set startValue = startValue + step
set i = i + 1
endloop
set i = 0
set j = j + 1
endloop
elseif whichMethod == METHOD_COL_WISE then
loop
exitwhen j >= m
loop
exitwhen i >= n
set this.matRow[i][j] = startValue
set startValue = startValue + step
set i = i + 1
endloop
set i = 0
set j = j + 1
endloop
endif
endmethod
method add takes Matrix mat returns Matrix
local Matrix result
local integer i = 0
local integer j = 0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "add", "Matrix", this, "Invalid Matrix!")
debug endif
debug if mat.n != this.n or mat.m != this.m then
debug call ThrowError(true, "Matrices", "add", "Matrix", this, "Matrices must be of same dimension!")
debug endif
set result = Matrix.create(n, m)
loop
exitwhen j >= n
loop
exitwhen i >= m
set result[j][i] = this.matRow[j][i] + mat[j][i]
set i = i + 1
endloop
set i = 0
set j = j + 1
endloop
return result
endmethod
method sub takes Matrix mat returns Matrix
local Matrix result
local integer i = 0
local integer j = 0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "sub", "Matrix", this, "Invalid Matrix!")
debug endif
debug if mat.n != this.n or mat.m != this.m then
debug call ThrowError(true, "Matrices", "sub", "Matrix", this, "Matrices must be of same dimension!")
debug endif
set result = Matrix.create(n, m)
loop
exitwhen j >= n
loop
exitwhen i >= m
set result[j][i] = this.matRow[j][i] - mat[j][i]
set i = i + 1
endloop
set i = 0
set j = j + 1
endloop
return result
endmethod
method multiply takes Matrix mat returns Matrix
local Matrix result
local integer i = 0
local integer j = 0
local integer k = 0
local real temp = 0.0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "multiply", "Matrix", this, "Invalid Matrix!")
debug endif
debug if this.m != mat.n then
debug call ThrowError(true, "Matrices", "multiply", "Matrix", this, "Matrix dimensions must agree!")
debug endif
set result = Matrix.create(n, mat.m)
loop
exitwhen j >= result.n
loop
exitwhen k >= result.m
loop
exitwhen i >= this.m
set temp = temp + this.matRow[j][i]*mat[i][k]
set i = i + 1
endloop
set result[j][k] = temp
set i = 0
set temp = 0.0
set k = k + 1
endloop
set k = 0
set j = j + 1
endloop
return result
endmethod
method transpose takes nothing returns Matrix
local Matrix mat = Matrix.create(m, n)
local integer i = 0
local integer j = 0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "transpose", "Matrix", this, "Invalid Matrix!")
debug endif
loop
exitwhen j >= m
loop
exitwhen i >= n
set mat[j][i] = this.matRow[i][j]
set i = i + 1
endloop
set i = 0
set j = j + 1
endloop
return mat
endmethod
method gauss takes nothing returns Matrix
local Matrix mat
local integer i = 0
local integer j = 0
local integer k = 0
local integer row
local real maxVal = -Math.Inf
local real pivot
debug if n < 1 then
debug call ThrowError(true, "Matrices", "gauss", "Matrix", this, "Invalid Matrix!")
debug endif
set mat = this.assign()
loop
exitwhen i >= n - 1
set j = i + 1
set row = i
loop
exitwhen j >= n
set pivot = Math.abs(mat[j][i])
if pivot > maxVal then
set maxVal = pivot
set row = j
endif
set j = j + 1
endloop
if row != i then
set j = 0
loop
exitwhen j >= m
set pivot = mat[i][j]
set mat[i][j] = mat[row][j]
set mat[row][j] = pivot
set j = j + 1
endloop
endif
set j = i + 1
loop
exitwhen j >= n
set pivot = mat[j][i]/mat[i][i]
set k = i
loop
exitwhen k >= n
set mat[j][k] = mat[j][k] - pivot*mat[i][k]
set k = k + 1
endloop
set j = j + 1
endloop
set i = i + 1
endloop
return mat
endmethod
method invert takes nothing returns Matrix
local Matrix mat
local Matrix inv
local integer i = 0
local integer j = 0
local integer k = 0
local integer row
local real maxVal = -Math.Inf
local real pivot
local real temp_inv
debug if n < 1 then
debug call ThrowError(true, "Matrices", "invert", "Matrix", this, "Invalid Matrix!")
debug endif
set mat = this.assign()
set inv = Matrix.create(n, n)
call inv.eye(n)
loop
exitwhen i >= n - 1
set j = i + 1
set row = i
loop
exitwhen j >= n
set pivot = Math.abs(mat[j][i])
if pivot > maxVal then
set maxVal = pivot
set row = j
endif
set j = j + 1
endloop
if row != i then
set j = 0
loop
exitwhen j >= m
set pivot = mat[i][j]
set mat[i][j] = mat[row][j]
set mat[row][j] = pivot
set temp_inv = inv[i][j]
set inv[i][j] = inv[row][j]
set inv[row][j] = temp_inv
set j = j + 1
endloop
endif
set j = i + 1
loop
exitwhen j >= n
set pivot = mat[j][i]/mat[i][i]
set k = 0
loop
exitwhen k >= n
set mat[j][k] = mat[j][k] - pivot*mat[i][k]
set inv[j][k] = inv[j][k] - pivot*inv[i][k]
set k = k + 1
endloop
set j = j + 1
endloop
set i = i + 1
endloop
set i = n - 1
loop
exitwhen i < 0
set j = i - 1
loop
exitwhen j < 0
set pivot = mat[j][i]/mat[i][i]
set mat[j][i] = mat[j][i] - pivot*mat[i][i]
set k = 0
loop
exitwhen k >= m
set inv[j][k] = inv[j][k] - pivot*inv[i][k]
set k = k + 1
endloop
set j = j - 1
endloop
set i = i - 1
endloop
set i = 0
loop
exitwhen i >= n
set j = 0
loop
exitwhen j >= m
set inv[i][j] = inv[i][j]/mat[i][i]
set j = j + 1
endloop
set i = i + 1
endloop
call mat.destroy()
return inv
endmethod
method trace takes nothing returns real
local integer i = 0
local integer minDim
local real result = 0.0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "trace", "Matrix", this, "Invalid Matrix!")
debug endif
if n <= m then
set minDim = n - 1
else
set minDim = m - 1
endif
loop
exitwhen i > minDim
set result = result + this.matRow[i][i]
set i = i + 1
endloop
return result
endmethod
method assign takes nothing returns Matrix
local integer i = 0
local integer j = 0
local Matrix mat = Matrix.create(n, m)
if n < 1 then
set mat = Invalid_Matrix
return mat
endif
loop
exitwhen i >= n
loop
exitwhen j >= m
set mat[i][j] = this.matRow[i][j]
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return mat
endmethod
method rank takes nothing returns integer
local Matrix mat = this.assign()
local integer minDim
local integer i
local integer rank
debug if n < 1 then
debug call ThrowError(true, "Matrices", "rank", "Matrix", this, "Invalid Matrix!")
debug endif
if n <= m then
set minDim = n - 1
else
set minDim = m - 1
endif
set i = minDim
set rank = minDim + 1
set mat = this.gauss()
loop
exitwhen i < 1
if Math.abs(mat[i][i]) < EPSILON then
set rank = rank - 1
endif
set i = i - 1
endloop
return rank
endmethod
method cond takes integer whichNorm returns real
local Matrix mat
local real result
debug if n < 1 then
debug call ThrowError(true, "Matrices", "cond", "Matrix", this, "Invalid Matrix!")
debug endif
set mat = this.assign()
set mat = this.multiply(mat.invert())
set result = mat.norm(whichNorm)
call mat.destroy()
return result
endmethod
method det takes nothing returns real
local Matrix mat
local integer i = 0
local real result = 1.0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "det", "Matrix", this, "Invalid Matrix!")
debug endif
debug if n != m then
debug call ThrowError(true, "Matrices", "det", "Matrix", this, "Matrix must be square!")
debug endif
set mat = this.assign()
set mat = mat.gauss()
loop
exitwhen i >= n
set result = result*mat[i][i]
set i = i + 1
endloop
if Math.abs(result) < EPSILON then
set result = 0.0
endif
call mat.destroy()
return result
endmethod
method solveSLE takes Matrix b returns Matrix
local Matrix mat
local Matrix sol
local Matrix x
local integer i = 0
local integer j = 0
local integer k = 0
local integer row
local real maxVal = -Math.Inf
local real pivot
debug if n < 1 then
debug call ThrowError(true, "Matrices", "solveSLE", "Matrix", this, "Invalid Matrix!")
debug endif
debug if this.n != this.m or b.n != this.n or b.m > 1 then
debug call ThrowError(true, "Matrices", "solveSLE", "Matrix", this, "Invalid Matrices used! Can't solve SLE!")
debug endif
set mat = this.assign()
set sol = b.assign()
set x = Matrix.create(b.n, 1)
loop
exitwhen i >= n - 1
set j = i + 1
set row = i
loop
exitwhen j >= n
set pivot = Math.abs(mat[j][i])
if pivot > maxVal then
set maxVal = pivot
set row = j
endif
set j = j + 1
endloop
if Math.abs(pivot) < EPSILON then
return Matrix.Invalid_Matrix
endif
if row != i then
set j = 0
loop
exitwhen j >= m
set pivot = mat[i][j]
set mat[i][j] = mat[row][j]
set mat[row][j] = pivot
set j = j + 1
endloop
set pivot = sol[i][0]
set sol[i][0] = sol[row][0]
set sol[row][0] = pivot
endif
set j = i + 1
loop
exitwhen j >= n
set pivot = mat[j][i]/mat[i][i]
set k = i
loop
exitwhen k >= n
set mat[j][k] = mat[j][k] - pivot*mat[i][k]
set k = k + 1
endloop
set sol[j][0] = sol[j][0] - pivot*sol[i][0]
set j = j + 1
endloop
set i = i + 1
endloop
set x[x.n - 1][0] = sol[x.n - 1][0]/mat[n - 1][n - 1]
set i = x.n - 2
loop
exitwhen i < 0
set pivot = sol[i][0]
set j = i + 1
loop
exitwhen j >= n
set pivot = pivot - mat[i][j]*x[j][0]
set j = j + 1
endloop
set x[i][0] = pivot/mat[i][i]
set i = i - 1
endloop
call sol.destroy()
call mat.destroy()
return x
endmethod
method norm takes integer whichNorm returns real
local integer i = 0
local integer j = 0
local real result
local real maxVal = -Math.Inf
debug if n < 1 then
debug call ThrowError(true, "Matrices", "norm", "Matrix", this, "Invalid Matrix!")
debug endif
debug if whichNorm != ONE_NORM and whichNorm != EUCLIDEAN_NORM and whichNorm != INFINITY_NORM then
debug call ThrowError(true, "Matrices", "[]", "Matrix", this, "Invalid Norm used!")
debug endif
if whichNorm == ONE_NORM then
set result = 0.0
loop
exitwhen i >= m
loop
exitwhen j >= n
set result = result + Math.abs(this.matRow[j][i])
set j = j + 1
endloop
if result > maxVal then
set maxVal = result
endif
set result = 0.0
set j = 0
set i = i + 1
endloop
return maxVal
elseif whichNorm == EUCLIDEAN_NORM then
set result = 0.0
loop
exitwhen i >= n
loop
exitwhen j >= m
set result = result + this.matRow[i][j]*this.matRow[i][j]
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return SquareRoot(result)
else
set result = 0.0
loop
exitwhen i >= n
loop
exitwhen j >= m
set result = result + Math.abs(this.matRow[i][j])
set j = j + 1
endloop
if result > maxVal then
set maxVal = result
endif
set result = 0.0
set j = 0
set i = i + 1
endloop
return maxVal
endif
endmethod
method dotProduct takes Matrix mat returns real
local real temp = 0.0
local integer i = 0
local integer j = 0
debug if n < 1 or mat.n < 1 then
debug call ThrowError(true, "Matrices", "dotProduct", "Matrix", this, "Invalid Matrix!")
debug endif
debug if mat.m != 1 or this.m != 1 then
debug call ThrowError(true, "Matrices", "dotProduct", "Matrix", this, "Dot-Product is only defined for Vectors!")
debug endif
debug if mat.n != this.n then
debug call ThrowError(true, "Matrices", "dotProduct", "Matrix", this, "Dot-Product is only defined for Vectors of same length!")
debug endif
loop
exitwhen i > n
set temp = temp + this.matRow[i][1]*mat[i][1]
set i = i + 1
endloop
return temp
endmethod
method crossProduct takes Matrix mat returns Matrix
local Matrix result
debug if n < 1 or mat.n < 1 then
debug call ThrowError(true, "Matrices", "crossProduct", "Matrix", this, "Invalid Matrix!")
debug endif
debug if mat.m != 1 or this.m != 1 then
debug call ThrowError(true, "Matrices", "crossProduct", "Matrix", this, "Cross-Product is only defined for Vectors!")
debug endif
debug if mat.n != this.n then
debug call ThrowError(true, "Matrices", "crossProduct", "Matrix", this, "Cross-Product is only defined for Vectors of same length!")
debug endif
debug if mat.n != 3 or this.n != 3 then
debug call ThrowError(true, "Matrices", "crossProduct", "Matrix", this, "This implementation only supports Cross-Products for Vectors in R^3")
debug endif
set result = Matrix.create(3, 1)
set result[0][0] = this.matRow[1][0]*mat[2][0] - this.matRow[2][0]*mat[1][0]
set result[1][0] = this.matRow[2][0]*mat[0][0] - this.matRow[0][0]*mat[2][0]
set result[2][0] = this.matRow[0][0]*mat[1][0] - this.matRow[1][0]*mat[0][0]
return result
endmethod
method reShape takes integer newN, integer newM, integer whichMethod returns Matrix
local Matrix mat
local integer i = 0
local integer j = 0
local integer row = 0
local integer col = 0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "reShape", "Matrix", this, "Invalid Matrix!")
debug endif
debug if newN*newM != n*m then
debug call ThrowError(true, "Matrices", "reShape", "Matrix", this, "Reshape not possible! Dimension missmatch!")
debug endif
debug if newN < 1 or newM < 1 then
debug call ThrowError(true, "Matrices", "reShape", "Matrix", this, "Reshape not possible! Index must be greater than zero!")
debug endif
debug if n == 0 then
debug call ThrowError(true, "Matrices", "reShape", "Matrix", this, "Reshape not possible! Matrix is invalid!")
debug endif
debug if whichMethod != METHOD_ROW_WISE and whichMethod != METHOD_COL_WISE then
debug call ThrowError(true, "Matrices", "reShape", "Matrix", this, "Invalid method for reshaping!")
debug endif
set mat = Matrix.create(newN, newM)
if whichMethod == METHOD_ROW_WISE then
loop
exitwhen i >= n
loop
exitwhen j >= m
set mat[row][col] = this.matRow[i][j]
set col = col + 1
if col >= mat.m then
set row = row + 1
set col = 0
endif
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
elseif whichMethod == METHOD_COL_WISE then
loop
exitwhen i >= m
loop
exitwhen j >= n
set mat[row][col] = this.matRow[j][i]
set col = col + 1
if col >= mat.m then
set row = row + 1
set col = 0
endif
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
endif
return mat
endmethod
method embed takes Matrix subMat, integer startRow, integer startCol returns Matrix
local Matrix mat
local integer i = 0
local integer j = 0
debug if n == 0 or subMat.n == 0 then
debug call ThrowError(true, "Matrices", "embed", "Matrix", this, "Can't embed sub Matrix! This is an invalid Matrix!")
debug endif
debug if startRow < 0 or startCol < 0 then
debug call ThrowError(true, "Matrices", "embed", "Matrix", this, "Can't merge Matrices! Index must be greater than 0!")
debug endif
debug if startRow + subMat.n - 1 > n or startCol + subMat.m - 1 > m then
debug call ThrowError(true, "Matrices", "embed", "Matrix", this, "Can't merge Matrices! Matrices don't fit!")
debug endif
set mat = this.assign()
loop
exitwhen i >= subMat.n
loop
exitwhen j >= subMat.m
set mat[i + startRow][j + startCol] = subMat[i][j]
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return mat
endmethod
method subMatrix takes integer startRow, integer startCol, integer endRow, integer endCol returns Matrix
local Matrix mat
local integer i = 0
local integer j = 0
debug if n == 0 then
debug call ThrowError(true, "Matrices", "subMatrix", "Matrix", this, "Can't determine sub Matrix! This is an invalid Matrix!")
debug endif
debug if endRow < startRow or endCol < startCol then
debug call ThrowError(true, "Matrices", "subMatrix", "Matrix", this, "Can't determine sub Matrix! Size of sub Matrix smaller 1 x 1!")
debug endif
debug if endRow > n - 1 or endCol > m - 1 then
debug call ThrowError(true, "Matrices", "subMatrix", "Matrix", this, "Sub Matrix exceeds Matrix dimensions!")
debug endif
set mat = Matrix.create(endRow - startRow + 1, endCol - startCol + 1)
loop
exitwhen i >= mat.n
loop
exitwhen j >= mat.m
set mat[i][j] = this.matRow[i + startRow][j + startCol]
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return mat
endmethod
method concatV takes Matrix mat returns Matrix
local Matrix result
local integer i = 0
local integer j = 0
debug if n == 0 or m == 0 then
debug call ThrowError(true, "Matrices", "concatV", "Matrix", this, "Can't concat Invalid Matrices!")
debug endif
debug if m != mat.m then
debug call ThrowError(true, "Matrices", "concatV", "Matrix", this, "Can't concat Matrices! Matrix column dimensions must be equal!")
debug endif
set result = Matrix.create(n + mat.n, m)
loop
exitwhen i >= n
loop
exitwhen j >= m
set result[i][j] = mat[i][j]
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
set i = 0
set j = 0
loop
exitwhen i >= n
loop
exitwhen j >= m
set result[i + n][j] = this.matRow[i][j]
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return result
endmethod
method concatH takes Matrix mat returns Matrix
local Matrix result
local integer i = 0
local integer j = 0
debug if n == 0 or m == 0 then
debug call ThrowError(true, "Matrices", "concatH", "Matrix", this, "Can't concat Invalid Matrices!")
debug endif
debug if n != mat.n then
debug call ThrowError(true, "Matrices", "concatH", "Matrix", this, "Can't concat Matrices! Matrix row dimensions must be equal!")
debug endif
set result = Matrix.create(n, m + mat.m)
loop
exitwhen i >= n
loop
exitwhen j >= m
set result[i][j] = this.matRow[i][j]
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
set i = 0
set j = 0
loop
exitwhen i >= n
loop
exitwhen j >= m
set result[i][j + m] = mat[i][j]
set j = j + 1
endloop
set j = 0
set i = i + 1
endloop
return result
endmethod
method switchRow takes integer whichRow, integer newRow returns nothing
local real temp
local integer i = 0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "switchRow", "Matrix", this, "Invalid Matrix!")
debug endif
debug if whichRow < 0 or whichRow >= n or newRow < 0 or newRow >= n then
debug call ThrowError(true, "Matrices", "switchRow", "Matrix", this, "Can't switch row. Index exceeds Matrix dimensions!")
debug endif
loop
exitwhen i >= this.m
set temp = this.matRow[newRow][i]
set this.matRow[newRow][i] = this.matRow[whichRow][i]
set this.matRow[whichRow][i] = temp
set i = i + 1
endloop
endmethod
method switchCol takes integer whichCol, integer newCol returns nothing
local real temp
local integer i = 0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "switchCol", "Matrix", this, "Invalid Matrix!")
debug endif
debug if whichCol < 0 or whichCol >= n or newCol < 0 or newCol >= n then
debug call ThrowError(true, "Matrices", "switchCol", "Matrix", this, "Can't switch column. Index exceeds Matrix dimensions!")
debug endif
loop
exitwhen i >= this.n
set temp = this.matRow[i][newCol]
set this.matRow[i][newCol] = this.matRow[i][whichCol]
set this.matRow[i][whichCol] = temp
set i = i + 1
endloop
endmethod
method display takes nothing returns nothing
local string s = ""
local integer i = 0
local integer j = 0
debug if n < 1 then
debug call ThrowError(true, "Matrices", "display", "Matrix", this, "Invalid Matrix!")
debug endif
loop
exitwhen j >= this.n
loop
exitwhen i >= this.m
set s = s + " " + R2S(this.matRow[j][i])
set i = i + 1
endloop
call DisplayTimedTextToPlayer(GetLocalPlayer(), 0.0, 0.0, 60.0, s)
set s = ""
set i = 0
set j = j + 1
endloop
endmethod
implement Inits
endstruct
endlibrary
JASS:
scope Example initializer Init
private function Init takes nothing returns nothing
/**********************************************************************************
*
* Example Code
* ¯¯¯¯¯¯¯¯¯¯¯¯
*
* Solves the Linear System of Equations A*x = b for
*
* [1][4][7] [x1] [1] [ 0]
* [17][5][8] * [x2] = [2] with the solution x = [ 2] approximately.
* [3][6][9] [x3] [3] [-1]
*
* Feel free to try out more.
*
**********************************************************************************/
// Create a 3 x 3 system Matrix A
local Matrix A = Matrix.create(3, 3)
// Create a 3 x 1 solution Vector b
local Matrix b = Matrix.create(3, 1)
// Instanciate the unknown Vector x
local Matrix x
// Initialize Matrix A in ascending order (col-wise)
call A.initStepWise(1.0, 1.0, Matrix.METHOD_COL_WISE)
// Set the element in the second row, first column of A to 17.0
set A[1][0] = 17.0
// Initialize Vector b (row-wise)
call b.initStepWise(1.0, 1.0, Matrix.METHOD_ROW_WISE)
// Solve SLE
set x = A.solveSLE(b)
// Display A, b and x
call A.display()
call DisplayTimedTextToPlayer(GetLocalPlayer(), 0.0, 0.0, 60.0, " ")
call b.display()
call DisplayTimedTextToPlayer(GetLocalPlayer(), 0.0, 0.0, 60.0, " ")
call x.display()
endfunction
endscopeMatrix struct
[] operatorsUse the [] operators to access directly to the values of a given Matrix. For example mat[2][1] will return the element in the third row, second column. Note that the indices are, like Wc3 arrays, zero-based.
readonly integer nSpecifies the number of rows of a given Matrix.
readonly integer mSpecifies the number of columns of a given Matrix.
readonly static Matrix Invalid_MatrixAn invalid Matrix of the size 0 x 0. You can't create such a Matrix, so if you need one, use this field. Some algorithms, such as solveSLE return such a Matrix if no solution for a given System of Linear Equations could be found. You can use the method isValid() to determine wether a Matrix is valid or not.
static constant integer ONE_NORMUse this as a parameter for the norm method to specify that the method should calculate the one norm (maximum of column sum absolute values).
static constant integer EUCLIDEAN_NORMUse this as a parameter for the norm method to specify that the method should calculate the euclidean norm (square root of sum of squares).
static constant integer INFINITY_NORMUse this as a parameter for the norm method to specify that the method should calculate the infinity norm (maximum of row sum absolute values).
static constant integer METHOD_ROW_WISEUse this as a parameter for methods like initStepWise or reShape to specify whether the method should be applied row-wise.
static constant integer METHOD_COL_WISEUse this as a parameter for methods like initStepWise or reShape to specify whether the method should be applied col-wise.
static method create takes integer nDim, integer mDim returns MatrixCreates a new n x m Matrix with the maximum size of MAX_MATRIX_SIZE (specified in the globals block). The Matrix is initialized with zeros.
method destroy takes nothing returns nothingDestroys a given Matrix to free its memory usage.
method display takes nothing returns nothingUse this method to display a Matrix ingame. This is especially meant for debugging issues.
method isValid takes nothing returns booleanChecks whether a given Matrix is valid (means: not empty) or not.
method isEqual takes Matrix mat returns booleanChecks whether two Matrices are equal or not. If A == B then A.isEqual(B) returns true.
method init takes real value returns nothingUse this method to initialize a Matrix with a desired real value. Note that this method does not create a new instance of the Matrix object, as well as all methods that only initialize the values of a Matrix.
method eye takes nothing returns nothingUse this method to initialize an Identity Matrix.
method diag takes real value, integer whichDiagonal returns nothingUse this method to initialize a Diagonal Matrix with a desired real value. Use the second argument to specify which diagonal you want to set (zero is the main diagonal, negative values address the upper, positive values the lower diagonals).
method rand takes real lowerBound, real upperBound returns nothingUse this method to initialize a Matrix with random real values.
method initStepWise takes real startValue, real steps returns nothingUse this method to initialize a matrix from a given start value in ascending or descending order specified by the steps parameter.
method assign takes nothing returns MatrixUse this method to assign a Matrix to another Matrix. For example set B = A.assign() will copy A to B. Note that A and B must be of equal size for this operation to work.
method addScalar takes real value returns MatrixThis method performs a element-wise addition of a given real value and returns the new Matrix. Example: A.addScalar(2.0) will add the value 2.0 to all elements of the Matrix A.
method subScalar takes real value returns MatrixThis method performs a element-wise subtraction of a given real value.
method mulScalar takes real value returns MatrixThis method performs a element-wise multiplication by a given real value.
method divScalar takes real value returns MatrixThis method performs a element-wise division by a given real value.
method abs takes nothing returns MatrixThis method performs the abs function on all Matrix elements.
method add takes Matrix whichMatrix returns MatrixMatrix addition. The expression A.add(B) where both A and B are Matrices returns the resulting Matrix A + B. Note that the Matrices must follow common Matrix calculation rules, like here that A and B have the same size.
method sub takes Matrix whichMatrix returns MatrixMatrix substraction. Same as the add method, A.sub(B) performs A - B.
method multiply takes Matrix whichMatrix returns MatrixMatrix multiplication. The expression A.multiply(B) performs the operation A*B. Note that A's number of columns must equal B's number of rows for this operation to be well-defined.
method transpose takes nothing returns MatrixMatrix transposition. The expression A.transpose() computes A^T.
method invert takes nothing returns MatrixMatrix inversion. Use A.invert() to calculate A^-1, the inverse of the Matrix A. Be aware of the fact that not every Matrix is invertable.
method gauss takes nothing returns MatrixUse this method to perform a Gauss-Elimination with pivotising. The result is a upper triangular Matrix.
method solveSLE takes Matrix b returns MatrixUse this method to solve a System of Linear Equations following the common notation A*x = b. To calculate x use A.solveSLE(b) where A is the system Matrix and b is the solution vector. If the SLE has no unique solution, an invalid vector of size 0 x 0 is returned.
method dotProduct takes Matrix b returns realUse this method to calculate the dot product of two Vectors. Use it like a.dotProduct(b), which results in a^T*b. Calling this method is faster than performing the transposition manualy and should therefore be used if possible. To check whether two Vectors are orthogonal, the dot product must be zero.
method crossProduct takes Matrix b returns MatrixUse this method to calculate the cross product of two Vectors. This implementation only supports calculation of cross products for Vectors in R^3.
method trace takes nothing returns realReturns the trace of a given Matrix. Which is defined as the sum over its diagonal elements.
method det takes nothing returns realReturns the determinant of a given Matrix. From A.det() == 0 follows for example that A is not invertable.
method rank takes nothing returns integerReturns the rank of a given Matrix. A square Matrix must have full rank to be invertable, which means that A.rank() == A.n must return true.
method norm takes integer whichNorm returns realComputes the norm of a given Matrix. You can choose between different norms by using the constants defined in the Matrix struct. Valid values for the whichNorm parameter are ONE_NORM, EUCLIDEAN_NORM and the INFINITY_NORM.
method cond takes integer whichNorm returns realComputes the condition of a Matrix. You can specify which Norm you want to use for that purpose by the parameter whichNorm (see method norm). Note that the Matrix must be invertable otherwise the condition will be infinity.
method subMatrix takes integer startRow, integer startCol, integer endRow, integer endCol returns MatrixThis method can be used to get a sub Matrix out of another Matrix. With the parameters startRow and startCol you can specify where the submatrix should begin and the parameters endRow as well as endCol define where to end the sub Matrix. If A is for example a 3 x 3 Matrix, A.subMatrix(0, 0, 2, 0) will return the first column Vector of A, while A.subMatrix(0, 0, 1, 1) will return the first 2 x 2 sub Matrix of A and so on.
method embed takes Matrix subMat, integer startRow, integer startCol returns MatrixThis method embeds one Matrix into another. If you have for example the 3 x 3 Matrix A and the 2 x 2 Matrix B then A.embed(B, 0, 0) will assign the upper left sub matrix of A to the values of B. The parameters startRow and startCol specify where the embeding should start. Of course the sub matrix must fit into the Matrix you want to embed it into, otherwise an error will be thrown.
method concatH takes Matrix mat returns MatrixUse this method to concatenate two Matrices. The Matrices must have the same amount of rows for this operation to work. The Matrices will get concatenated horizontal, resulting for two n x m Matrices in a n x 2*m Matrix. Example: A.concatH(B) will concatenate A to B (from the left side).
method concatV takes Matrix mat returns MatrixUse this method to concatenate two Matrices. The Matrices must have the same amount of columns for this operation to work. The Matrices will get concatenated vertically, resulting for two n x m Matrices in a 2*n x m Matrix. Example: A.concatV(B) will stack the Matrix B on A.
method reShape takes integer newN, integer newM, integer whichMethod returns MatrixUse this method to reshape a Matrix. If you have for example a 3 x 2 Matrix A, by performing A.reShape(2, 3, METHOD_ROW_WISE) the Matrix will get a 2 x 3 Matrix. The third parameter whichMethod determines whether the operation should be done row-wise or column-wise. METHOD_ROW_WISE and METHOD_COL_WISE are valid parameters. This can also be used to make a Vektor of a Matrix (or vice versa): A.reShape(6, 1, METHOD_COL_WISE) will stack all column Vektors of A to one 6 x 1 Vektor.
method switchRow takes integer whichRow, integer newRow returns MatrixUse this method to switch two different rows of a Matrix. The expression A.switchRow(0, 2) will switch the first with the third row. Note that both parameters whichRow and newRow must not exceed Matrix dimensions.
method switchCol takes integer whichCol, integer newCol returns MatrixUse this method to switch two different columns of a Matrix. Same rules as for switchRow apply here.
4. Screenshots
Enclosed are some screenshots of the testmap, showing some of the ingame calculations from the MathParser Extension.



5. Accuracy and Performance
The following tables show the accuracy of the natural logarithm function which is used to calculate al other logarithms as well as the hyperbolic functions and their inverses. Also performance for all math functions is displayed in an extra table. Finally the efficiency of the isPrime method is analysed and compared towards the standard brute force attempt.
As it is shown in the following table, the logarithm reaches extremly high accuracies. This is important because
many other functions can be computed by using logarithms, therefore high acuracy is required. The logarithm
functions Ln1 to Ln5 from the table were taken from this Snippet by BlinkBoy.

The following table shows the OP-Limit values for new math functions. As the table shows, nearly all functions
are very efficient and can be used without any problems. Critical methods in terms of performance are isPrime,
mergeFloat and the factorial of an integer number.

The diagram shows the efficiency of the isPrime method. The system uses a deterministic version of the Miller-
Rabin test. While the standard brute-force attempt can only detect primes up to ~5003 before it hits the OP-Limit,
this method can detect much higher primes. As the diagram shows, the OP-Limit is quite alternating but stays
basically at the same mean. This method allows to detect primes efficiently up to ~100000.

Hope you enjoy it!
Greetings,
lfh
Keywords:
Advanced Mathematics, Math, Calculator, Ingame calculator, interpreter, logarithm, hyperbolic
Contents
Reviews
Similar threads
- Locked

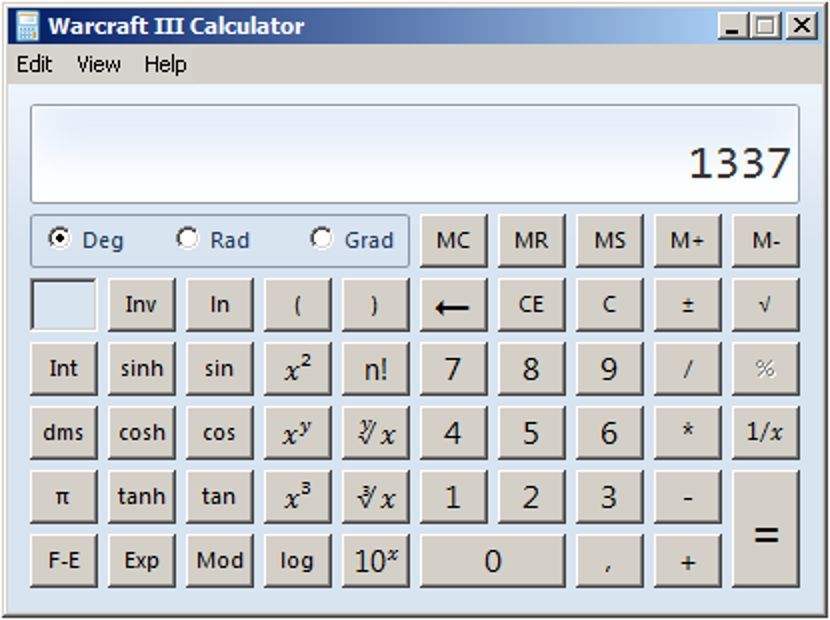
 Approved
Approved




















