- Joined
- Nov 11, 2004
- Messages
- 1,986
(Disclaimer: I'm not sure if someone has presented this method before, if he has please inform me, I just developed this today and I've been unable to check).
EDIT: I checked, and most of the other methods are different some use binary, others borzan. The method which i found to use the same first rule that I apply, is pipedream's from wc3jass. Credits to him since he posted the idea first, .
.
Logarithm:
I scripted 5 functions for calculating the natural logarithm of a number, the first one is slower than the later, but it's more accurate.
The earlier functions work only for values between [1,+infinite)
The next functions are a bit slower but have a full dominious of logarithm: (0,+inifinite)
I'll explain a bit what's done.
The first part of the function takes care of calculating the integer part of the logarithm. We keep divinding our number by the base(e), until our number is smaller than e.
a good way to observe it is in this way:
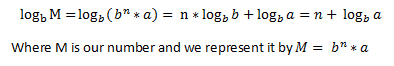
As you see, we percieve the number as a multiplication. Now, why did we make this?(Here's where most of you get lost) Very simple, when calculating the definate integral of a function which we can't calculate through normal algebra, we must use the Simpson's method. Why I didn't use it directly? Simpson's rule is an approximation of the definite integral, the bigger be the distance between a and b(the range of the integral), the biggger will be the accumulated error.
Some of you may remenber that the derivate of the natural logarithm is an hyperbole: Ln'(x) = 1/x (d(Ln(x))/dx = 1/x). 1/x is a function which is calculateable through normal aritmethics. Now knowing that, we can calculate the definate integral between 1 and the leaving value, which is < e, using Simpson's Rule.
I'm not going to be very specific on Simpson's rule, you can look at it in wikipedia or mathworld.
Now the Benchmarking and Statistics:
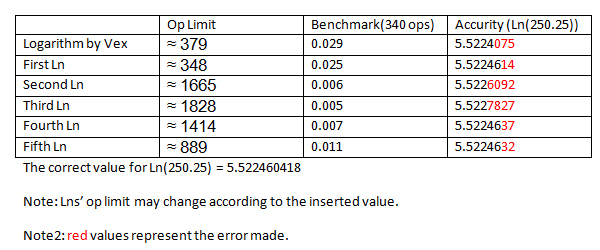
Here's anotther test with an smaller number:
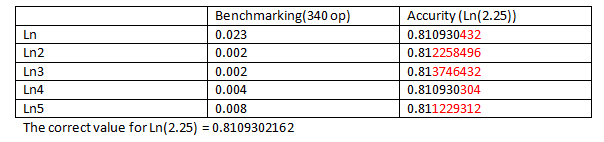
It will be your decision to decide which function you'll use. I would suggest Third for fast usage, like for moving objects or places where you need it a lot. The fourth one should be used for things that do require a LOT of accurity, like armor calculation. I would suggest to scrap the first and fifth they were just propositions to solve the problem.
EDIT: forgot to mention it, because I thought it was obvious. The O of our f(x) is O(ln (n)) in all the functions, notice that not every algorithm to calculate Ln(n) has the same growth as the function. For instance, Vexorian's logarithm has a constant speed growth because it approximates the functions by using borzan acotation every set of predefined interations.
EDIT: I checked, and most of the other methods are different some use binary, others borzan. The method which i found to use the same first rule that I apply, is pipedream's from wc3jass. Credits to him since he posted the idea first,
Logarithm:
I scripted 5 functions for calculating the natural logarithm of a number, the first one is slower than the later, but it's more accurate.
JASS:
function Ln takes real a returns real
local real s = 1.0
local real sum = 0.0
local real g
local real e
local integer i = 10
loop
exitwhen a < bj_E
set a = a/bj_E
set sum = sum + 1.
endloop
set e = (a-1.0)/10. //quite accurate for numbers < e
set g = s + e
loop
exitwhen i <= 0 or a <= 1.0
set i = i-1
set sum = sum + (g-s)*(1./s + 8./(s+g) + 1./g)/6.
set s = g
set g = s + e
endloop
return sum
endfunction
// cubic, very good accurity for warcraft
function Ln takes real a returns real
local real sum = 0.0
loop
exitwhen a < bj_E
set a = a/bj_E
set sum = sum + 1.
endloop
return sum + (a-1.)*(1. + 9./(2.+a) + 9./(1.+a*2.) + 1./a)/8.
endfunction
//Even faster! --parabollic, has a good accurity as well
function Ln takes real a returns real
local real sum = 0.0
loop
exitwhen a < bj_E
set a = a/bj_E
set sum = sum + 1.
endloop
return sum + (a-1.)*(1. + 8./(1.+ a) + 1./a)/6.
endfunction
//Fourth, this one is quite a bit more accurate than the former 2, but it is a bit slower.
function Ln takes real a returns real
local real sum = 0.0
local real e = 1.284025
loop
exitwhen a < bj_E
set a = a/bj_E
set sum = sum + 1.
endloop
loop
exitwhen a < e
set a = a/e
set sum = sum + .25
endloop
return sum + (a-1.)*(1. + 8./(1.+ a) + 1./a)/6. //and we apply simpson's :D
endfunction
//Added a Fifth, this one uses Taylor series instead.
function Ln takes real a returns real
local real sum = 0.0
local real e = 1.648721
local real b
loop
exitwhen a < bj_E
set a = a/bj_E
set sum = sum + 1.
endloop
if a >= e then
set a = a/e
set sum = sum + .5
endif
//Time to apply Taylor series of ln(1+x).
set e = 1.
set a = (a - 1.)
set b = a
loop
exitwhen e > 5.
set sum = sum + a/e
set e = e + 1.
set a = a*b*(-1.)
endloop
return sum
endfunction
function LogB takes real a, real base returns real
return Ln(a)/Ln(base) //I would suggest that you save the nautral log of the base
//if you want to keep using it over and over.
endfunction
JASS:
define {
FOURTH_E = 1.284025
}
float Ln(float a) {
float sum = 0.0;
loop {
exitwhen a < bj_E;
a /= bj_E;
sum+=1.; //I don't trust ++ for reals ¬¬
}
return sum + (a-1.)*(1. + 8./(1.+ a) + 1./a)/6.;
}
float Ln(float a) {
float sum = 0.0;
loop {
exitwhen a < bj_E;
a /= bj_E;
sum+=1.; //I don't trust ++ for reals ¬¬
}
loop {
exitwhen a < FOURTH_E;
a /= FOURTH_E;
sum+=.25;
}
return sum + (a-1.)*(1. + 8./(1.+ a) + 1./a)/6.;
}
float LogB(float a, float b) {
return Ln(a)/Ln(b);
}
Code:
const fixed math_e = 2.7182818;
const fixed math_e_p4 = 1.284025;
fixed Ln(fixed val) {
fixed sum = 0.0;
while (val < math_e) {
val /= math_e;
sum+=1.;
}
while (val < math_e_p4) {
val /= math_e_p4;
sum+=.25;
}
return sum + (val-1.)*(1. + 8./(1.+ val) + 1./val)/6.;
}
int Log2(int val) {
int i = 0;
while(val > 1) {
val >>= 1;
i += 1;
}
return i;
}The earlier functions work only for values between [1,+infinite)
The next functions are a bit slower but have a full dominious of logarithm: (0,+inifinite)
JASS:
//Even faster! --parabollic, has 2 decimals accurity
function Ln takes real a returns real
local real sum = 0.0
local real sign = 1.
if a < 1. then
set a = 1./a
set sign = -1.
endif
loop
exitwhen a < bj_E
set a = a/bj_E
set sum = sum + 1.
endloop
return sign*(sum + (a-1.)*(1. + 8./(1.+ a) + 1./a)/6.)
endfunction
//Fourth, this one is quite a bit more accurate than the former 2, but it is a bit slower.
//5 decimals accurity.
function Ln takes real a returns real
local real sum = 0.0
local real sign = 1.
if a < 1. then
set a = 1./a
set sign = -1.
endif
loop
exitwhen a < bj_E
set a = a/bj_E
set sum = sum + 1.
endloop
loop
exitwhen a < 1.284025
set a = a/1.284025
set sum = sum + .25
endloop
return sign*(sum + (a-1.)*(1. + 8./(1.+ a) + 1./a)/6.) //and we apply simpson's :D
endfunction
JASS:
define {
FOURTH_E = 1.284025
}
float Ln(float a) {
float sum = 0.0;
float sign = 1.;
if a < 1. { a = 1./a; sign = -1. }
loop {
exitwhen a < bj_E;
a /= bj_E;
sum+=1.; //I don't trust ++ for reals ¬¬
}
return sign*(sum + (a-1.)*(1. + 8./(1.+ a) + 1./a)/6.);
}
float Ln(float a) {
float sum = 0.0;
float sign = 1.;
if a < 1. { a = 1./a; sign = -1. }
loop {
exitwhen a < bj_E;
a /= bj_E;
sum+=1.; //I don't trust ++ for reals ¬¬
}
loop {
exitwhen a < FOURTH_E;
a /= FOURTH_E;
sum+=.25;
}
return sign*(sum + (a-1.)*(1. + 8./(1.+ a) + 1./a)/6.);
}I'll explain a bit what's done.
The first part of the function takes care of calculating the integer part of the logarithm. We keep divinding our number by the base(e), until our number is smaller than e.
a good way to observe it is in this way:
As you see, we percieve the number as a multiplication. Now, why did we make this?(Here's where most of you get lost) Very simple, when calculating the definate integral of a function which we can't calculate through normal algebra, we must use the Simpson's method. Why I didn't use it directly? Simpson's rule is an approximation of the definite integral, the bigger be the distance between a and b(the range of the integral), the biggger will be the accumulated error.
Some of you may remenber that the derivate of the natural logarithm is an hyperbole: Ln'(x) = 1/x (d(Ln(x))/dx = 1/x). 1/x is a function which is calculateable through normal aritmethics. Now knowing that, we can calculate the definate integral between 1 and the leaving value, which is < e, using Simpson's Rule.
I'm not going to be very specific on Simpson's rule, you can look at it in wikipedia or mathworld.
Now the Benchmarking and Statistics:
Here's anotther test with an smaller number:
It will be your decision to decide which function you'll use. I would suggest Third for fast usage, like for moving objects or places where you need it a lot. The fourth one should be used for things that do require a LOT of accurity, like armor calculation. I would suggest to scrap the first and fifth they were just propositions to solve the problem.
EDIT: forgot to mention it, because I thought it was obvious. The O of our f(x) is O(ln (n)) in all the functions, notice that not every algorithm to calculate Ln(n) has the same growth as the function. For instance, Vexorian's logarithm has a constant speed growth because it approximates the functions by using borzan acotation every set of predefined interations.
Attachments
Last edited by a moderator:






