- Joined
- Dec 19, 2009
- Messages
- 1,039
(30 ratings)
 Approved
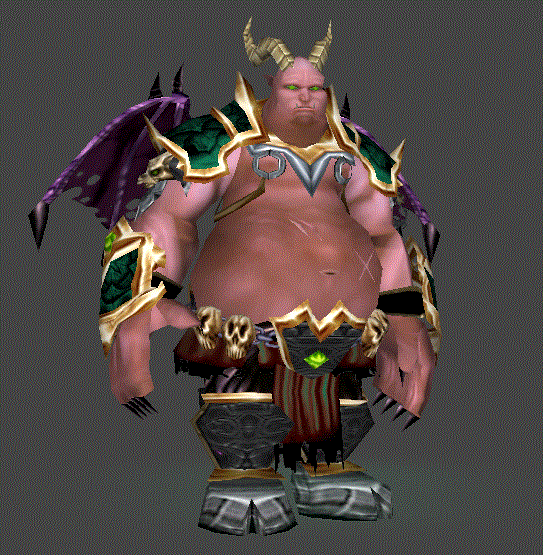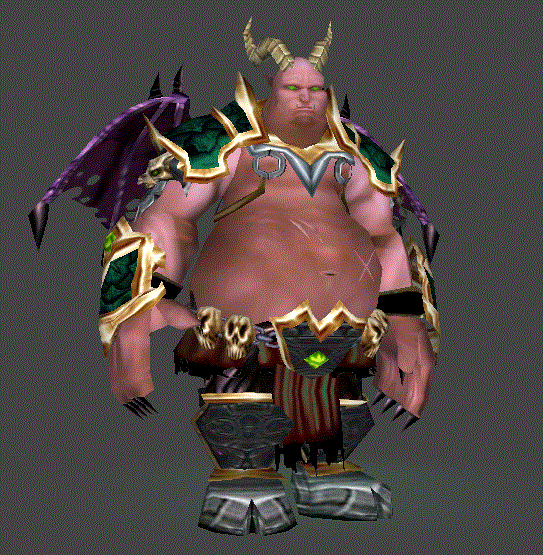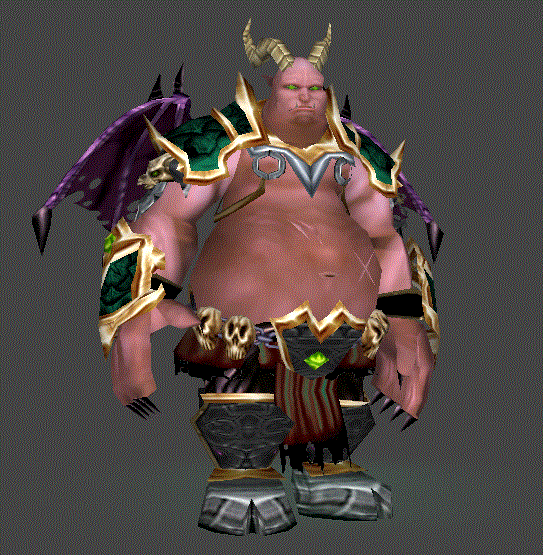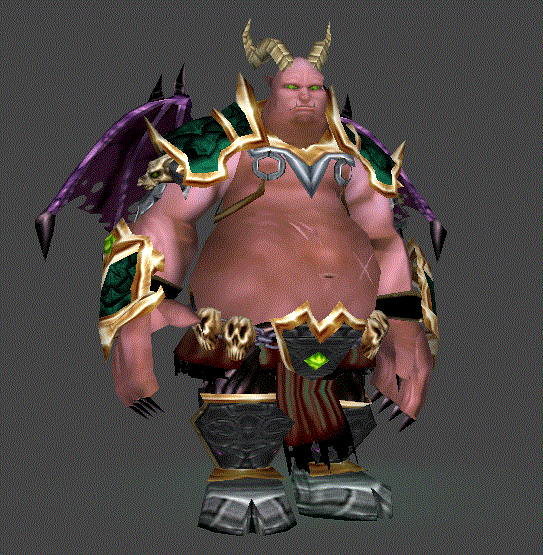
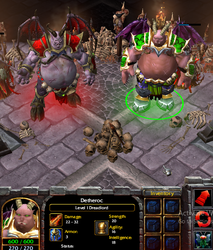
Approvedwhy not?Warcraft 3 Reforged has been released a year ago and I am still trying to understand the reason why they decided to make a fat dreadlord.
Exactly. I mean, I was hoping to see a fat version of paladin too.why not?
I kinda agree. I also never liked that texture, but without separating the parts of the mesh and make the wrapping look 'blocky' I cannot wrap it right. Color wise, as long as I know there is not a texture that would fit the the color Detheroc has in the reforged. I was thinking the cinematic Illidan texture for the body, but it's too muscular and again I would need to geoset color it.I think this model would benefit greatly if you would use a more contrasty texture instead of the wow-like/low contrast human campaign texture. I understand its appeal because its easy to wrap and one of (if not the only) human skin texture that has all the muscles and limbs connected to a whole body, without it having anything on it. But I never really liked it, because it was always just too non-contrasty and people tend to geoset-color it, which makes it even worse.
Otherwise its a mighty fine model.
Edit: Now that I looked at it again, my point grows even stronger, as the skin texture does not match the wings skin and creates a very noticable difference between the two.
Edit 2: Also would help a great deal if you re-wrap the shin and feet-armor, as it is very streteched & flat right now and hurts the overall appearance, as everything else is very neatly and tidely wrapped.

Added a version with different texture for the wings.Dude, this is insane!
But i think that would be better if you make the texture of the wings and the body of the same color.
Chungus Uther when?Exactly. I mean, I was hoping to see a fat version of paladin too.

Warcraft 3 Reforged has been released a year ago and I am still trying to understand the reason why they decided to make a fat dreadlord.
This could work if Detheroc was a boss in one of those videogames where there are some characters that represent the Seven Deadly Sins, in which Detheroc was, of course, Gluttony.