Rotation Functions

[Nestharus]

I know I kind of left, but I figured that I'd post something useful

The y and z are swapped (like most game engines).

I'll probably add little demo on how to calculate the interception point between two velocities. It's actually pretty simple.

I'll also probably put up some quaternion functions that you can use with CalculateAngleRotation.

Here's a sweet post on it -> http://forum.onlineconversion.com/showpost.php?p=41014&postcount=2

http://lolengine.net/blog/2013/09/18/beautiful-maths-quaternion-from-vectors

I saw that someone posted a resource for 2D. Here's 3D. Enjoy. I made this because I needed it for an assignment and a lot of the online equations are wrong -.-. They are all over the place. These are the working equations. Yes, I took the few minutes to solve them after my laziness failed >.>.

If anyone wants to understand how they work

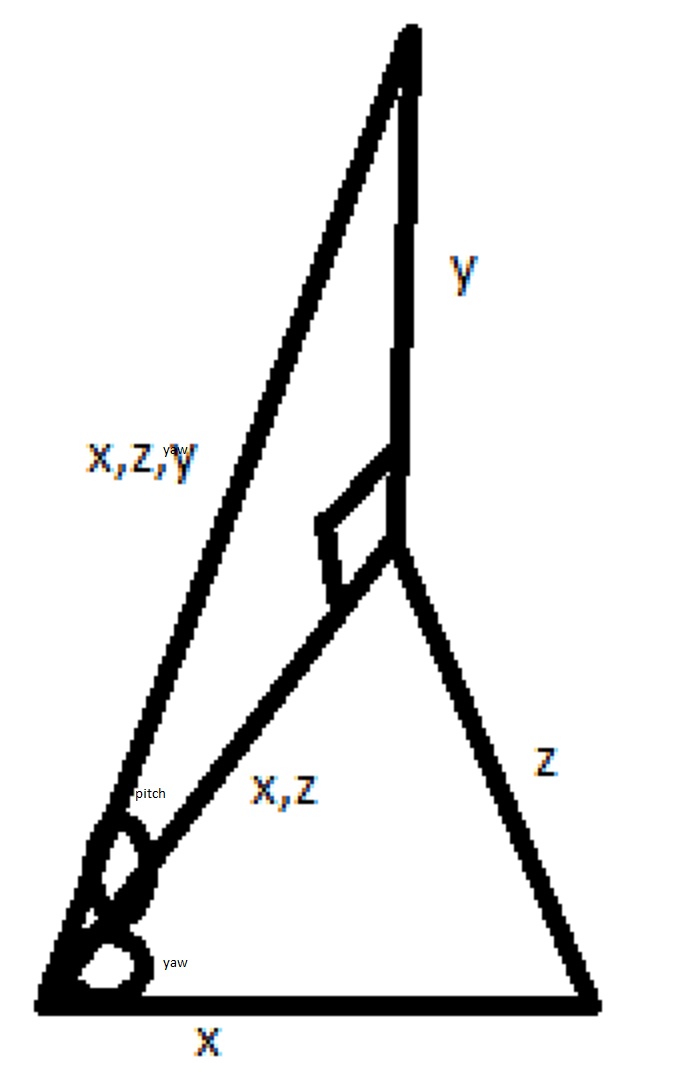
Keep in mind that Sin and Cos return fractions. You can multiply fractions together to get a fraction of a fraction. How would you get x in that picture given yaw and pitch? x is a fraction of xz, which is a fraction of xzy. xz is the Cos component of xzy. x is the Cos component of xz. xz = xzy*cos(pitch). x = xz*cos(yaw). How would you get y and z?

To understand rotate towards, take a look at a unit circle. Just google trig circle. From there, work it out yourself . It works : P. Keep in mind that unit vectors are those x,y components, so comparing unit vectors directly will also work. However, you'll still have to return the angle and apply the rotation to the vector based on angles ;(. The extra cosine and sine are overhead, but they make the function more understandable. I guess I could add a between points version of it. See the end of this post to understand how checking the unit vectors would work . Remember, pitch is composed of two fun vectors, xz and y!

function SetUnitYaw takes unit whichUnit, real radians returns nothing
    call SetUnitFacing(whichUnit, radians*57.2957795)
endfunction


function GetUnitYaw takes unit whichUnit returns real
    return GetUnitFacing(whichUnit)/57.2957795
endfunction


function RotateUnitYaw takes unit whichUnit, real radians returns nothing
    call SetUnitYaw(whichUnit, GetUnitYaw(whichUnit) + radians)
endfunction

//to work with pitch, use Vexorian's dummy.mdl
//this is buggy because vexorian's dummy.mdl doesn't go all the way around. It should go from 0-360, not 0-180.
//with the model as it is now, you can't have upside down units
function SetUnitPitch takes unit whichUnit, real radians returns nothing
    local integer i = R2I(radians*57.2957795 + 90.5)
     
    if (i > 179) then
        set i = 179
    elseif (i < 0) then
        set i = 0
    endif

    //should store current pitch into an array
    //set unit____currentPitch[GetUnitUserData(whichUnit)] = radians
    call SetUnitAnimationByIndex(whichUnit, i)
endfunction


function GetUnitPitch takes unit whichUnit returns real
    //return the value in that array
    return //unit____currentPitch[GetUnitUserData(whichUnit)]
endfunction


function RotateUnitPitch takes unit whichUnit, real radians returns nothing
    call SetUnitPitch(whichUnit, GetUnitPitch(whichUnit) + radians)
endfunction
 
//the next three functions are used to convert a yaw and pitch to
//a unit vector representing the direction
function CalculateDirectionX takes real yaw, real pitch returns real
    return Cos(yaw)*Cos(pitch)
endfunction


function CalculateDirectionY takes real pitch returns real
    return Sin(pitch)
endfunction


function CalculateDirectionZ takes real yaw, real pitch returns real
    return Sin(yaw)*Cos(pitch)
endfunction

//the next two functions are used to calculate yaw and pitch from a
//vector representing direction (does not have to be a unit vector)
function CalculateVectorYaw takes real x, real z returns real
    return Atan2(z, x)
endfunction


function CalculateVectorPitch takes real x, real y, real z returns real
    return Atan2(y, SquareRoot(x*x + z*z))
endfunction


function CalculateVectorMagnitude takes real x, real y, real z returns real
    return SquareRoot(x*x + y*y + z*z)
endfunction

//howMuchPitchToRotateBy = CalculateAngleRotation(myAngle, myDesiredAngle, myPitchTurnRate)
//HowMuchYawToRotateBy = CalculateAngleRotation(myAngle, myDesiredAngle, myYawTurnRate)
//RotateUnitYaw(myUnit, howMuchYawToRotateBy)
//RotateUnitPitch(myUnit, howMuchPitchToRotateBy)
function CalculateAngleRotation takes real currentAngle, real targetAngle, real turnRate returns real
    if (Cos(currentAngle - targetAngle) < Cos(turnRate)) then
        if (0 < Sin(currentAngle - targetAngle)) then
            return -turnRate 
        else
            return turnRate
        endif
    endif

    return targetAngle - currentAngle
endfunction

edit
given a unit vector current and a target unit vector target and a max angular rotation Cos(rotation)

current.x - target.x < angular rotation?
0 < current.z - target.z?

pitch would use the magnitude of xz as x and y as z

current.xz - target.xz < angular rotation?
0 < current.y - target.y?

the problem is returning the angle

 

[Menag]

If anyone wants to understand how they work, remember that Sin/Cos/Tan return fractions and think about a sphere with y pointing up, x pointing right, and z pointing to you. The vector on the xz plane is the hypotenuse of the triangle with sides x,z. If you include y, then the triangle of xzy has sides xz,y. The x and z use sines and cosines together because, once again, they are fractions. The hypotenuse is the x component of the big triangle with angle pitch. The x is the cosine component of that hypotenuse. Hence x = cos(yaw)*cos(pitch). z = sin(yaw)*cos(pitch) for the same reason, it is the y component of that hypotenuse. y only does sin(pitch) because it's the y component of the pitch . Just think of fractions of fractions. You take a fraction of the big big hypotenuse to get the small hypotenuse, then you take a fraction of that to get to x,z.

That's actually just the so called parametrization of the unit sphere. You wrote
(cos(phi)cos(theta), sin(phi)cos(theta), sin(theta)).
(You can also exchange cos(theta) with sin(theta) and vice-versa)

One can explain this more easyly. First look at the x and y component and the angle phi. There you have (cos(phi), sin(phi)). This is the parametrization of the unitcircle. Phi is the angle beginning at the x-axis and going counterclockwise. Theta is now the angle beginning at the northpole and going downwards (Yes I took z going upwards because wc3 does so too and this is actually how you do it in mathematics). I'm too stupid to paint something right now but here's some beautiful picture from the german wikipedia:
http://commons.wikimedia.org/wiki/File:Sphere_3d.png
I hope this is a better explaination.

 

[Ezekiel12]

For kind of this question I joined here. Never got a real answer though.

Is this also applicable to texture translation/rotation using quaternions? I guess yes..
Its just sad that no model editor I tried could show texture rotations..

But knowing exactly how to do it is a big plus.

 

[Bannar]

The highest resolution picture I've seen in a while. I belive its PS with some advanced tuning o?

 

[GhostWolf]

For kind of this question I joined here. Never got a real answer though.

Is this also applicable to texture translation/rotation using quaternions? I guess yes..
Its just sad that no model editor I tried could show texture rotations..

But knowing exactly how to do it is a big plus.

No, quaternions work a little differently with vector rotation than the above Euler angles.
Assuming you have some quaternion q and a vector v and you want to rotate v by q, then the equation is q^-1 * v * q, where q^-1 is the conjugate of q.

Since you mentioned texture rotations, do you have a model with those?

 

[Ezekiel12]

Since you mentioned texture rotations, do you have a model with those?

Yes, for example ui/feedback/cooldown/ui-cooldown-indicator.mdx uses all kinds of texture animation. Thats also the model I wanted to edit.

 

[GhostWolf]

Yes, for example ui/feedback/cooldown/ui-cooldown-indicator.mdx uses all kinds of texture animation. Thats also the model I wanted to edit.

Interesting, I'll see if I am not too lazy to add rotation support to the model viewer. Not that there will ever be user-made models using them, since no editor supports them, but just for completeness' sake.

 

[Ezekiel12]

Interesting, I'll see if I am not too lazy to add rotation support to the model viewer. Not that there will ever be user-made models using them, since no editor supports them, but just for completeness' sake.

Well for example Magos supports all kinds of texture animation but IIRC just cant show texture rotation.

Mhm, so you are in charge or the Warcraft 3 Viewer, interesting...

 

[GhostWolf]

Well for example Magos supports all kinds of texture animation but IIRC just cant show texture rotation.

Mhm, so you are in charge or the Warcraft 3 Viewer, interesting...

WC3ME only works (visually) with translations, the same as the viewer. By model viewer I mean the one here on the hive, not the application.

Never saw any model with scaling or rotation keys until now, so I didn't bother implementing them. Maybe one day I'll wake up less lazy and implement rotation, I put it in my TODO list.

 

[Cokemonkey11]

I usually prefer working with the trig identities/vectors directly, but this could be a useful reference for beginners. Maybe convert this to tutorial form?

//to work with pitch, use Vexorian's dummy.mdl
//this is buggy because vexorian's dummy.mdl doesn't go all the way around. It should go from 0-360, not 0-180.
//with the model as it is now, you can't have upside down units
function SetUnitPitch takes unit whichUnit, real radians returns nothing
local integer i = R2I(radians*57.2957795 + 90.5)

if (i > 179) then
set i = 179
elseif (i < 0) then
set i = 0
endif

//should store current pitch into an array
//set unit____currentPitch[GetUnitUserData(whichUnit)] = radians
call SetUnitAnimationByIndex(whichUnit, i)
endfunction

You can sort of hack around it using two units as I did a couple years ago with this - http://www.xfire.com/videos/53ef10 (hard to see at low frame rate)

Also, I think someone could make a new version of dummy.mdx with a full axis of rotation.