projectile parabolic movement

[NightStalker]

So guys, i've been working on a custom spell which fires a projectile from above and lands on the target point.

The question is, can any of you guys come up with a formula that i can use for the projectile. It should move like this

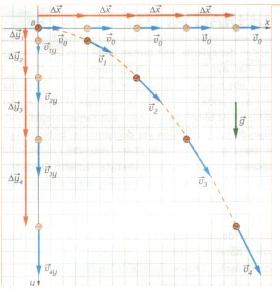
but it should use variables like current height, distance to the target...

 

[Licheus]

y(x) = 0,25x² is the function for this parable.

To use this in a meaningful way within our context we could do something like this: if we for example want the projectile to spawn 100 distance from its target, our function tells us that we'll want to give the projectile a starting height of 625. y(100) = (0,25 * 100)² = 25² = 625.

I suggest that you choose a multiple of 4 as the distance between your projectile spawn and the target location of the spell. For example, you could create the projectile dummy at 180 to the direct right of the target location and set it to start at 2025 height (according to our function).

For our movement trigger we do this: create a trigger that runs at an interval, let's say every 0.02 seconds. For every interval move the projectile 4 closer to the target location of the spell. Add 4 to a variable for distance travelled. Then set the height of the projectile to 2025 - (distance travelled * 0.25)².

Is this a meaningful approach to you or did you have something else in mind?

 

[muzzel]

I think he wants the formula for a parabola given a height (where the projectile is starting) and a distance (to the target) so the projectile will hit the target.
In general your parabola has the equation:
y(x) = a*x^2
where a is some parameter. Given a fixed height, for larger a the projectile fly a longer distance. y denotes the height, where 0 is the initial height for the projectile and positive values denote a position below 0.
By selecting the correct a you can make sure the projectile hit the target. To hit the target the following equation must be true:
y(distance) = height
so
a = height/distance^2

 

[Adiktuz]

I think he wants the formula for a parabola given a height (where the projectile is starting) and a distance (to the target) so the projectile will hit the target.
In general your parabola has the equation:
y(x) = a*x^2
where a is some parameter. Given a fixed height, for larger a the projectile fly a longer distance. y denotes the height, where 0 is the initial height for the projectile and positive values denote a position below 0.
By selecting the correct a you can make sure the projectile hit the target. To hit the target the following equation must be true:
y(distance) = height
so
a = height/distance^2

given your formula, at fixed height, larger "a" will actually mean shorter distance...

@OP - btw, you would still need to translate it into wc3's coordinates... y here will become Z while X will actually be composed of (x,y)... look for some threads using parabola or projectile as keyword, there are posts of the actual usable wc3 computation for parabolic movement...

 

[gorillabull]

i think he wants to do 3d projectile movement in which case the xy parabola wont do

 

[muzzel]

As Adiktuz said he has to convert it to 3d. Its fairly simple:
- For y you use z (in wc3 coordinates z always denotes the height)

- Instead of x you use the distance in the x/y plane, which is a 2d vector.
Lets say your projectile starts at (px, py, pz) and your target is at (tx, ty, tz). Then the distance on the x/y plane is d = (dx, dy) = (tx-px, ty-py).
To use this distance with the formula i posted you can just calculate the length of d (using the normal L2 norm):
|d| = sqrt(dx^2 + dy^2)

Calculate a:
a = height/|d|^2
which is equal to:
a = heigth/(dx^2 + dy^2)

The formula for the parabola:
z(x, y) = a*(x^2 + y^2)

However its probably easier to parametrize the whole thing, so instead of using a formula of the type z(x, y) we use three formulas, x(t), y(t), z(t) where t is the parameter of the time. Then the question is how to determine the missile speed.
1. You want constant missile speed, so higher distance = projectile takes more time to reach target
2. You want a fixed flying time for the missile, so higher distance = faster missile
Tell me if its 1. or 2. and i can provide jass code.

 

[NightStalker]

y(x) = 0,25x² is the function for this parable.

To use this in a meaningful way within our context we could do something like this: if we for example want the projectile to spawn 100 distance from its target, our function tells us that we'll want to give the projectile a starting height of 625. y(100) = (0,25 * 100)² = 25² = 625.

I suggest that you choose a multiple of 4 as the distance between your projectile spawn and the target location of the spell. For example, you could create the projectile dummy at 180 to the direct right of the target location and set it to start at 2025 height (according to our function).

For our movement trigger we do this: create a trigger that runs at an interval, let's say every 0.02 seconds. For every interval move the projectile 4 closer to the target location of the spell. Add 4 to a variable for distance travelled. Then set the height of the projectile to 2025 - (distance travelled * 0.25)².

Is this a meaningful approach to you or did you have something else in mind?

this seems good but how do i get the distance travelled i couldnt find a formula for that too :S

As Adiktuz said he has to convert it to 3d. Its fairly simple:
- For y you use z (in wc3 coordinates z always denotes the height)

- Instead of x you use the distance in the x/y plane, which is a 2d vector.
Lets say your projectile starts at (px, py, pz) and your target is at (tx, ty, tz). Then the distance on the x/y plane is d = (dx, dy) = (tx-px, ty-py).
To use this distance with the formula i posted you can just calculate the length of d (using the normal L2 norm):
|d| = sqrt(dx^2 + dy^2)

Calculate a:
a = height/|d|^2
which is equal to:
a = heigth/(dx^2 + dy^2)

The formula for the parabola:
z(x, y) = a*(x^2 + y^2)

However its probably easier to parametrize the whole thing, so instead of using a formula of the type z(x, y) we use three formulas, x(t), y(t), z(t) where t is the parameter of the time. Then the question is how to determine the missile speed.
1. You want constant missile speed, so higher distance = projectile takes more time to reach target
2. You want a fixed flying time for the missile, so higher distance = faster missile
Tell me if its 1. or 2. and i can provide jass code.

and for this first one is what i need. If you can provide it can you put general comments that explains the formula too?

 

[Licheus]

this seems good but how do i get the distance travelled i couldnt find a formula for that too :S

Distance travelled is in this case just a variable of type Real. When our projectile spawns, the distance travelled variable should be 0. In my example above, we move the the projectile by 4 distance towards its impact location every interval. Then every interval we should also add 4 to our distance travelled variable. This will make our variable hold the exact distance that the projectile has travelled, and it will be updated correctly.

Another way of getting distance travelled is this:
projectile distance travelled = (distance between (projectile current point) and (projectile target point)) - (distance between (projectile spawn point) and (projectile target point)). I guess this is the formula you're looking for here? The variable solution takes less processing power though.

Visual representation

 

[NightStalker]

wow nice explanation thanks
Actually i should figure out the formula but i don't know why i can't even think about anything my mind's stuck and doesn't work (

i'll use this formula and after that i'll try the parabola thing. Thanks for helping