- Joined
- Sep 22, 2007
- Messages
- 2,772
Introduction
Pitch and Roll are two extremely useful object data fields usable for many object data fields. This tutorial will focus entirely on the usage of doodads and destructibles. They can seem relatively complex when starting out to use them, but actually, they are quite simple. The two fields allow you to tilt an object, forwards and sideways, so as to put different angles to use, tilt normal things to show gravity shifts; there are hundreds of uses for this application.
I've also found that a lot of people either have no idea how they work or only have a vague idea - using random numbers of any kind of silly thing to limit their usage of these tools. Therefore, this should be good for anyone who wants to understand the Pitch and Roll Angle fields better.
In this tutorial, I'll be showing you the basics of the usage of positive numbers, which allow you to tilt objects to the angle of the terrain, and then moving onto a technical, mathematical explanation of the ideas behind the use of negative numbers, which will allow you to tilt objects at will on flat ground.
All you need to know for this is a basic understanding of the conversion of radians and degrees - this will be covered in the negative number section. Note that understanding of some mathematical concepts would help.
Note that the test doodad in this tutorial is a unit model, but not actually a unit. It was simply for the convenience of showing the turning well.
I: Positive Numbers
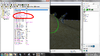
These are the fields we are talking about.
Positive numbers are quite a simple tool. Basically, they allow the user to tilt doodads/destructibles according to the gradient of the terrain. The almost only usage of this is to set both fields to 3.14 (as you might notice - this is pi). What this does is allow the maximum angle of pitch and roll of the doodad in relation to the normal, flat floor on a gradient to be a very high amount (180 degrees to be exact).
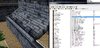
Because, practically speaking, no wall in WC3 modding is actually at a 90 degree angle to the ground, it is technically more than you need and therefore all that you need. If all that went over your head in technicality -- the unit will simply pitch and roll to the angle and gradient of the terrain, as in this picture:
Note how the Proudmoore model on the right hand side is at an exact perpendicular angle to the ground. This is allowed by the high maximum angle of pitch/roll in relation to a flat floor.
The differences between the Pitch and Roll angles are not particularly important in positive values as the process and everything is quite simple. Once the mathematical ideas behind this stuff are elaborated on, you can do your own (though limited) positive number pitching and rolling as well.
II: Negative Numbers
Negative numbers are the fun stuff of pitching and rolling things. Firstly, a guide to the actual impacts of pitch/roll:

These two lines show the path that your doodad's position will take as you increase/decrease the negative value of Max Pitch/Roll Angle. In the picture, the black line represents the Pitch Angle whereas the red represents the Roll Angle. Note that the position of the origin (of your unit) does not change. only the actual model. Simply imagine that the Proudmoore model's head will move along those lines as you change just one value and between them as you change both values.
Now, before we can start on the actual work, you need to understand the interchangeable concept of radians and degrees.
Radians and degrees are simply different ways of saying the same thing. While degrees go from 0-360 in a circle, radians go from 0-2 π. By the same token, in both instances, 0 = 360; 0 = 2 π.
You can change from degrees to radians by the formula of: "x * (π/180)" where x = your degrees and π = 3.14
This works backwards too: "x * (180/
π)" converts x radians into degrees.
So, with this idea in your mind, some important degrees/radians are:
2 π = 6.28 = 360
1.5 π = 4.71 = 270
1 π = 3.14 = 180
0.5 π = 1.57 = 90
0 π = 0 (==) 2 pi = 360
Therefore we move onto the next concept, which might seem obvious to you already by now. Pitch and Roll Angles have directions. These are determined in a simple way.

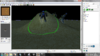
In this picture, firstly, there is a green line. This green line is running from the ORIGIN, the exact centre of the two circles of Pitch (Black) and Roll (Red), to the point decided by the Roll and Pitch of your doodad. They are, in a way, values of X and Y, with a constant value of Z that is simply the height of your model. Your model simply wraps around the green line. It is the green line for all intents and purposes.
As well as this, two arrows have been added. This is to show the direction that Pitching and Rolling occurs in - 'higher' negative values (lower values overall) will move it further along that direction.
Now we can get to the actual pitching and rolling. Firstly, you need to have your world editor allow you to use negative values. You can configure this in File>Preferences>General. To actually enter a negative value, you have to hold SHIFT while clicking the field, then enter the value with a - before it to make it negative. You HAVE to hold SHIFT while going into the value.
All that negative values do is move the tip of your green line, the top of your model to the given values. They will do this normally on flat ground, if the ground is angled, it will become confusing because the original picture is tilted and all sorts of weird things happen to the result. In my experience, it usually turns them opposite.
First, we'll change the Max Pitch Angle to -0.786 - 0.25 π - 45 degrees. This will change our base model's green line to a 45 degree inclination towards the floor.
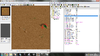
As shown, Proudmoore moves as expected. Everything is going good. You can increase this value up to 6.29 before it begins to start again. However, if you want to move him 45 degrees in the other direction, you'd have to subtract the 45 degrees / 0.25 π (0.786) from 6.29 - so therefore, this would have to be 5.50. In this way, the direction of the rotation is extremely important to know.
Next, we'll add the Roll in as well. This time, we'll move Proudmoore 90 degrees, therefore he should move partially into the floor - but not quite, because of the only 45 degree angle tilt on the Pitch. 90 degrees are 0.5 π, which makes for -1.57 as a value to put into the Max Roll Angle.

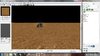
Again, he moves as desired. Since both pitch and roll have now been used, you can see how each field affects the doodad in question and how you can manipulate it to your best purposes. The best way to get familiar with all this stuff is to simply experiment. Know that it is extremely useful to know all this, both in playable terrain and art terrain.


For example - in the first picture, the bridge and vines are tilted. In the second, the walls, bridge and vines are. These are just some of the possible uses you could put this to, the only limit is your imagination.
Further exampels:


Pitch and Roll are two extremely useful object data fields usable for many object data fields. This tutorial will focus entirely on the usage of doodads and destructibles. They can seem relatively complex when starting out to use them, but actually, they are quite simple. The two fields allow you to tilt an object, forwards and sideways, so as to put different angles to use, tilt normal things to show gravity shifts; there are hundreds of uses for this application.
I've also found that a lot of people either have no idea how they work or only have a vague idea - using random numbers of any kind of silly thing to limit their usage of these tools. Therefore, this should be good for anyone who wants to understand the Pitch and Roll Angle fields better.
In this tutorial, I'll be showing you the basics of the usage of positive numbers, which allow you to tilt objects to the angle of the terrain, and then moving onto a technical, mathematical explanation of the ideas behind the use of negative numbers, which will allow you to tilt objects at will on flat ground.
All you need to know for this is a basic understanding of the conversion of radians and degrees - this will be covered in the negative number section. Note that understanding of some mathematical concepts would help.
Note that the test doodad in this tutorial is a unit model, but not actually a unit. It was simply for the convenience of showing the turning well.
I: Positive Numbers

These are the fields we are talking about.
Positive numbers are quite a simple tool. Basically, they allow the user to tilt doodads/destructibles according to the gradient of the terrain. The almost only usage of this is to set both fields to 3.14 (as you might notice - this is pi). What this does is allow the maximum angle of pitch and roll of the doodad in relation to the normal, flat floor on a gradient to be a very high amount (180 degrees to be exact).
Because, practically speaking, no wall in WC3 modding is actually at a 90 degree angle to the ground, it is technically more than you need and therefore all that you need. If all that went over your head in technicality -- the unit will simply pitch and roll to the angle and gradient of the terrain, as in this picture:

Note how the Proudmoore model on the right hand side is at an exact perpendicular angle to the ground. This is allowed by the high maximum angle of pitch/roll in relation to a flat floor.
The differences between the Pitch and Roll angles are not particularly important in positive values as the process and everything is quite simple. Once the mathematical ideas behind this stuff are elaborated on, you can do your own (though limited) positive number pitching and rolling as well.
II: Negative Numbers
Negative numbers are the fun stuff of pitching and rolling things. Firstly, a guide to the actual impacts of pitch/roll:

These two lines show the path that your doodad's position will take as you increase/decrease the negative value of Max Pitch/Roll Angle. In the picture, the black line represents the Pitch Angle whereas the red represents the Roll Angle. Note that the position of the origin (of your unit) does not change. only the actual model. Simply imagine that the Proudmoore model's head will move along those lines as you change just one value and between them as you change both values.
Now, before we can start on the actual work, you need to understand the interchangeable concept of radians and degrees.
Radians and degrees are simply different ways of saying the same thing. While degrees go from 0-360 in a circle, radians go from 0-2 π. By the same token, in both instances, 0 = 360; 0 = 2 π.
You can change from degrees to radians by the formula of: "x * (π/180)" where x = your degrees and π = 3.14
This works backwards too: "x * (180/
π)" converts x radians into degrees.
So, with this idea in your mind, some important degrees/radians are:
2 π = 6.28 = 360
1.5 π = 4.71 = 270
1 π = 3.14 = 180
0.5 π = 1.57 = 90
0 π = 0 (==) 2 pi = 360
Therefore we move onto the next concept, which might seem obvious to you already by now. Pitch and Roll Angles have directions. These are determined in a simple way.

In this picture, firstly, there is a green line. This green line is running from the ORIGIN, the exact centre of the two circles of Pitch (Black) and Roll (Red), to the point decided by the Roll and Pitch of your doodad. They are, in a way, values of X and Y, with a constant value of Z that is simply the height of your model. Your model simply wraps around the green line. It is the green line for all intents and purposes.
As well as this, two arrows have been added. This is to show the direction that Pitching and Rolling occurs in - 'higher' negative values (lower values overall) will move it further along that direction.
Now we can get to the actual pitching and rolling. Firstly, you need to have your world editor allow you to use negative values. You can configure this in File>Preferences>General. To actually enter a negative value, you have to hold SHIFT while clicking the field, then enter the value with a - before it to make it negative. You HAVE to hold SHIFT while going into the value.
All that negative values do is move the tip of your green line, the top of your model to the given values. They will do this normally on flat ground, if the ground is angled, it will become confusing because the original picture is tilted and all sorts of weird things happen to the result. In my experience, it usually turns them opposite.
First, we'll change the Max Pitch Angle to -0.786 - 0.25 π - 45 degrees. This will change our base model's green line to a 45 degree inclination towards the floor.

As shown, Proudmoore moves as expected. Everything is going good. You can increase this value up to 6.29 before it begins to start again. However, if you want to move him 45 degrees in the other direction, you'd have to subtract the 45 degrees / 0.25 π (0.786) from 6.29 - so therefore, this would have to be 5.50. In this way, the direction of the rotation is extremely important to know.
Next, we'll add the Roll in as well. This time, we'll move Proudmoore 90 degrees, therefore he should move partially into the floor - but not quite, because of the only 45 degree angle tilt on the Pitch. 90 degrees are 0.5 π, which makes for -1.57 as a value to put into the Max Roll Angle.


Again, he moves as desired. Since both pitch and roll have now been used, you can see how each field affects the doodad in question and how you can manipulate it to your best purposes. The best way to get familiar with all this stuff is to simply experiment. Know that it is extremely useful to know all this, both in playable terrain and art terrain.


For example - in the first picture, the bridge and vines are tilted. In the second, the walls, bridge and vines are. These are just some of the possible uses you could put this to, the only limit is your imagination.
Further exampels:


Last edited: