- Joined
- Feb 4, 2009
- Messages
- 1,314
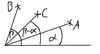
I'd like to have a formula which gives me the coordinates of the point C in this picture:
As you can see point B is rotated by angle alpha (can you say "rotated by vector A"?) around the origin so that it represents point C.
In other words the angle from A is subtracted from B to create C.
The function will be called very often so it mustn't contain cos/sin/tan/acos/asin/atan/sqrt and so on.
I've done this for 2D already but I need it for 3D. Anyway here is the 2D formula so it is easier for you to help me.
a, b and c are the length of the line from 0/0 to A, B and C
A, B and a are given
1.
Ax = a*cos(alpha) <=> Ax/a = cos(alpha)
Ay = a*sin(alpha) <=> Ay/a = sin(alpha)
2.
Bx = b*cos(beta) <=> Bx/b = cos(beta)
By = b*sin(beta) <=> By/b = sin(beta)
3.
Cx = b*cos(beta - alpha)
Cy = b*sin(beta - alpha)
4.
cos(beta - alpha) = cos(alpha)*cos(beta) + sin(alpha)*sin(beta)
sin(beta - alpha) = sin(alpha)*cos(beta) - cos(alpha)*sin(beta)
5.
4. into 3.:
Cx = b*(cos(alpha)*cos(beta) + sin(alpha)*sin(beta))
Cy = b*(sin(alpha)*cos(beta) - cos(alpha)*sin(beta))
6.
1. into 5.:
Cx = b*(Ax/a*cos(beta) + Ay/a*sin(beta))
Cy = b*(Ay/a*cos(beta) - Ax/a*sin(beta))
7.
2. into 6.:
Cx = b*(Ax/a*Bx/b + Ay/a*By/b)
Cy = b*(Ay/a*Bx/b - Ax/a*By/b)
8.
removing b:
Cx = Ax/a*Bx + Ay/a*By
Cy = Ay/a*Bx - Ax/a*By
Of course B/a can be extracted to make it faster.
Thanks if you read the text above until here and thanks in advance if you try to help me and another thanks if you make it work.
edit:
just noticed that I have to define towards which axis the angle will be subtracted
it should be the z-axis
also this might be helpful
http://www.hiveworkshop.com/forums/...l-code-snippets-40758/index9.html#post1917333

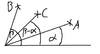
As you can see point B is rotated by angle alpha (can you say "rotated by vector A"?) around the origin so that it represents point C.
In other words the angle from A is subtracted from B to create C.
The function will be called very often so it mustn't contain cos/sin/tan/acos/asin/atan/sqrt and so on.
I've done this for 2D already but I need it for 3D. Anyway here is the 2D formula so it is easier for you to help me.
a, b and c are the length of the line from 0/0 to A, B and C
A, B and a are given
1.
Ax = a*cos(alpha) <=> Ax/a = cos(alpha)
Ay = a*sin(alpha) <=> Ay/a = sin(alpha)
2.
Bx = b*cos(beta) <=> Bx/b = cos(beta)
By = b*sin(beta) <=> By/b = sin(beta)
3.
Cx = b*cos(beta - alpha)
Cy = b*sin(beta - alpha)
4.
cos(beta - alpha) = cos(alpha)*cos(beta) + sin(alpha)*sin(beta)
sin(beta - alpha) = sin(alpha)*cos(beta) - cos(alpha)*sin(beta)
5.
4. into 3.:
Cx = b*(cos(alpha)*cos(beta) + sin(alpha)*sin(beta))
Cy = b*(sin(alpha)*cos(beta) - cos(alpha)*sin(beta))
6.
1. into 5.:
Cx = b*(Ax/a*cos(beta) + Ay/a*sin(beta))
Cy = b*(Ay/a*cos(beta) - Ax/a*sin(beta))
7.
2. into 6.:
Cx = b*(Ax/a*Bx/b + Ay/a*By/b)
Cy = b*(Ay/a*Bx/b - Ax/a*By/b)
8.
removing b:
Cx = Ax/a*Bx + Ay/a*By
Cy = Ay/a*Bx - Ax/a*By
Of course B/a can be extracted to make it faster.
Thanks if you read the text above until here and thanks in advance if you try to help me and another thanks if you make it work.

edit:
just noticed that I have to define towards which axis the angle will be subtracted
it should be the z-axis
also this might be helpful
http://www.hiveworkshop.com/forums/...l-code-snippets-40758/index9.html#post1917333
Attachments
Last edited: