- Joined
- May 2, 2019
- Messages
- 15
It has recently come to my attention that a number of ParabolaZ functions are incorrect, or rather, they are only accurate if the initial Z level and final Z level are identical - or if the maximum height value is sufficiently greater than either of the Z values.
Take for example, the popular ParabolaZ function:
When h (height) is close to either y0 or y1 (initial and final Z), the actual maximum height of the generated parabola will be incorrect.
From some looking around, I've discovered most if not all other ParabolaZ functions are just a variant of this, some with and some without the starting/end Z values as inputs.
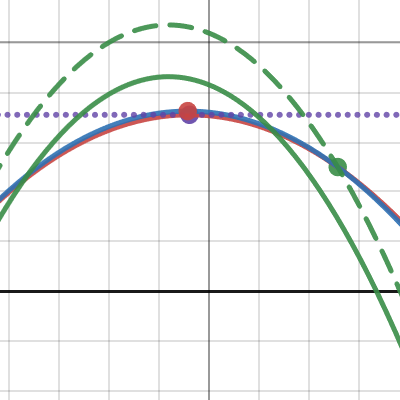
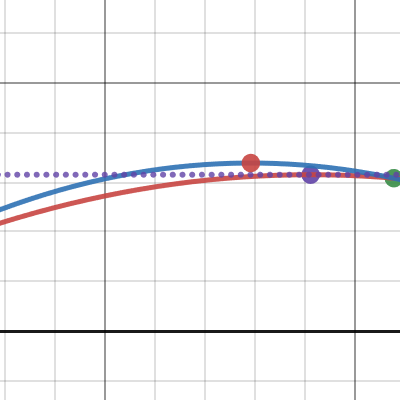
I've created a Desmos graph demonstrating a more accurate formula for determining the A and B constants of a parabola, and the difference between the popular method, and the more precise calculus derived method. My function of course, does not support having a height value inbetween the starting or ending Z level - as mathematically speaking, there is no real solution where a maximum/minimum height value could fall between those two.
 www.desmos.com
Unfortunately, the more accurate version of the equation may be significantly slower, requiring the usage of two SquareRoot calls, and some additional if/else branching to determine the sign of, essentially demanding that the function only be used to generate the A and B constants once, and stored for later usage in calculating the Z level.
www.desmos.com
Unfortunately, the more accurate version of the equation may be significantly slower, requiring the usage of two SquareRoot calls, and some additional if/else branching to determine the sign of, essentially demanding that the function only be used to generate the A and B constants once, and stored for later usage in calculating the Z level.
I've also included a variation of the inaccurate formula for use when the height value is "invalid" - so that the function does not result in a thread crash from taking the square root of a negative number but still returns a (mostly) serviceable result.
If there was actually an accurate ParabolaZ function somewhere out there, please let me know so that I can link it, so that someone else who is also searching for accurate parabolas might stumble onto it.
Also if anyone has additional ParabolaZ functions (with initial and ending Z values as inputs) - inaccurate or not, feel free to mention them so that I can include them in the comparison graph for future reference.
Edit: Fixed an error in the JASS code, mistook (h-y0)+(h-y1) and (h-y0)*(h-y1) when copying over the formula from the graphs.
Take for example, the popular ParabolaZ function:
JASS:
function ParabolaZ takes real y0, real y1, real h, real d, real x returns real
local real A = (2*(y0+y1)-4*h)/(d*d)
local real B = (y1-y0-A*d*d)/d
return A*x*x + B*x + y0
endfunctionFrom some looking around, I've discovered most if not all other ParabolaZ functions are just a variant of this, some with and some without the starting/end Z values as inputs.
I've created a Desmos graph demonstrating a more accurate formula for determining the A and B constants of a parabola, and the difference between the popular method, and the more precise calculus derived method. My function of course, does not support having a height value inbetween the starting or ending Z level - as mathematically speaking, there is no real solution where a maximum/minimum height value could fall between those two.

ParabolaZDemo
JASS:
function CalculateParabolaConstants takes real y0, real y1, real h, real d returns nothing
local real dh = h-y0
local real S = RSignBJ(dh)
local real hy= 2*h-y0-y1
if h > y0 and h < y1 then
//fall back to less accurate but more lenient equation
//call BJDebugMsg("Invalid height, undefined parabola value")
set udg_ParabolaA = (2*(y0+y1)-4*h)/(d*d)
set udg_ParabolaB = (-y1-3*y0+4*h)/d
else
set udg_ParabolaA = -1/(d*d)*(hy+2*S*SquareRoot((h-y0)*(h-y1)))
set udg_ParabolaB = S*SquareRoot(-4*udg_ParabolaA*dh)
endif
endfunctionIf there was actually an accurate ParabolaZ function somewhere out there, please let me know so that I can link it, so that someone else who is also searching for accurate parabolas might stumble onto it.
Also if anyone has additional ParabolaZ functions (with initial and ending Z values as inputs) - inaccurate or not, feel free to mention them so that I can include them in the comparison graph for future reference.
Edit: Fixed an error in the JASS code, mistook (h-y0)+(h-y1) and (h-y0)*(h-y1) when copying over the formula from the graphs.
Last edited: