Hello dear hive members.
The clock is now so many, and I really need to go too sleep. I have been up the whole night working on a exams project that needs to be finish in 8 hours.
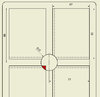
I got stuck one place, because Im not a math genius, so I hoped some one here can explain me, or just write down the line that will calculate
the red area on the picture below.
I need to know how big the red area you see on the picture are, so please
help if you know how to. I will be a GREAT help for me.
Thank you for your time
The clock is now so many, and I really need to go too sleep. I have been up the whole night working on a exams project that needs to be finish in 8 hours.
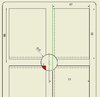
I got stuck one place, because Im not a math genius, so I hoped some one here can explain me, or just write down the line that will calculate
the red area on the picture below.
I need to know how big the red area you see on the picture are, so please
help if you know how to. I will be a GREAT help for me.
Thank you for your time