- Joined
- Jul 6, 2009
- Messages
- 1,885
In my map, i thought of using a simple 2D vector system with each vector having it's intensity and direction. Now i'm having problem summing 2 vectors.
I think i'm overcomplicating this, but here's the way i did it and it seems to return wrong values.
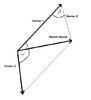
Given 2 vectors, i first determine which vector has greater angle so i have a geometric representation.

In the picture, i can find angle alpha since i have angles of vector 1 and 2. The beta angle is, from picture, 180 - alpha. With this, i used cosine law (c^2 = a^2 + b^2 - 2abcos(gamma) ) to determine result vector's intensity. Using sine law (a/sin(alpha) = b/sin(beta) = c/sin(gamma) ) i can determine angles between result vector and 2 vectors in which case i can add or subtract angles of 2 vectors to find the angle of resulting one
Is there another way or am i doing something wrong?
I think i'm overcomplicating this, but here's the way i did it and it seems to return wrong values.
Given 2 vectors, i first determine which vector has greater angle so i have a geometric representation.
In the picture, i can find angle alpha since i have angles of vector 1 and 2. The beta angle is, from picture, 180 - alpha. With this, i used cosine law (c^2 = a^2 + b^2 - 2abcos(gamma) ) to determine result vector's intensity. Using sine law (a/sin(alpha) = b/sin(beta) = c/sin(gamma) ) i can determine angles between result vector and 2 vectors in which case i can add or subtract angles of 2 vectors to find the angle of resulting one
Is there another way or am i doing something wrong?