- Joined
- Jul 10, 2007
- Messages
- 6,306
The spherical coordinate system maps points relative to an origin given two angles and a distance.
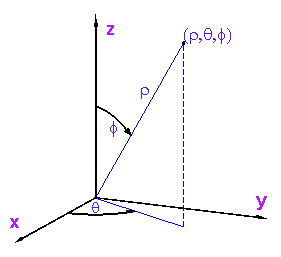
What makes this different from the Cartesian coordinate system is that rather than defining a point by its x,y,z distance from the origin, it defines a point by the magnitude of an x,y,z point and two angles (magnitude being distance).
The magnitude is defined as ||p|| or ||r|| = SquareRoot(x*x+y*y+z*z)
Notice how it has 3 dimensions. The z just needs to be added in order to get that third dimension.
The two angles define direction.
In the polar coordinate system, one angle and a distance is needed. This angle is theta, which is how far around a circle a given point goes.
Theta-

Note that because z is 0, it doesn't do anything in the polar coordinate system.
By adding a z, the magnitude expands and a second angle is needed, this angle being how far the point is from the northern z-axis (easier this way).
The range of phi goes from 0 to pi, 0 being north and pi being south.
In polar coordinates, phi is always pi/2.
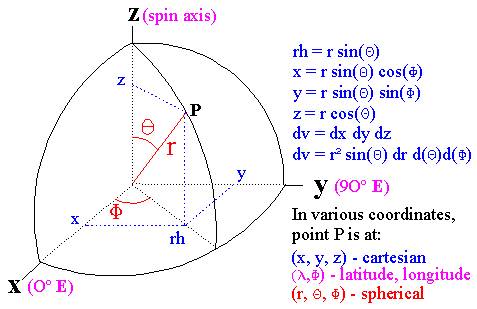
Equations are as follows
Angle Between Points (x0, y0, z0) and (x, y, z).
(x0, y0, z0) would be the first point
Distance between two 3D points
More information can be found at these sites

What makes this different from the Cartesian coordinate system is that rather than defining a point by its x,y,z distance from the origin, it defines a point by the magnitude of an x,y,z point and two angles (magnitude being distance).
The magnitude is defined as ||p|| or ||r|| = SquareRoot(x*x+y*y+z*z)
Notice how it has 3 dimensions. The z just needs to be added in order to get that third dimension.
The two angles define direction.
In the polar coordinate system, one angle and a distance is needed. This angle is theta, which is how far around a circle a given point goes.

Theta-
Code:
x = r*cos(theta)
y = r*sin(theta)
r = ||p|| = SquareRoot(x*x + y*y)
tan(theta) = y/xNote that because z is 0, it doesn't do anything in the polar coordinate system.
By adding a z, the magnitude expands and a second angle is needed, this angle being how far the point is from the northern z-axis (easier this way).
The range of phi goes from 0 to pi, 0 being north and pi being south.
In polar coordinates, phi is always pi/2.

Equations are as follows
Code:
x = p*cos(theta)*sin(phi)
y = p*sin(theta)*sin(phi)
z = p*cos(phi)
p = SquareRoot(x*x + y*y + z*z)
r = SquareRoot(x*x + y*y)
tan(theta) = y/x
tan(phi) = r/zAngle Between Points (x0, y0, z0) and (x, y, z).
(x0, y0, z0) would be the first point
Code:
where
----xd = x - x0
----yd = y - y0
----zd = z - z0
----pd = SquareRoot(xd*xd + yd*yd + zd*zd)
----rd = SquareRoot(xd*xd + yd*yd)
tan(theta) = yd/xd
tan(phi) = rd/zdDistance between two 3D points
Code:
where
----xd = x - x0
----yd = y - y0
----zd = z - z0
----pd = SquareRoot(xd*xd + yd*yd + zd*zd)
distance = pd
JASS:
thetaBetween = Atan2((y - y0), (x - x0))
phiBetween = Atan2(SquareRoot((x - x0)*(x - x0) + (y - y0)*(y - y0)), z - z0)
distanceBetween = SquareRoot((x - x0)*(x - x0) + (y - y0)*(y - y0) + (z - z0)*(z - z0))More information can be found at these sites
Last edited:







