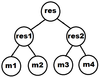
Let * be a binary, associative, commutative operation and M a set of elements for which * is defined.
Let S = m_1 * m_2 * m_3 * ... * m_n for m_i ∈ M.
I need a data structure for M that allows easy recalculation of S when:
- one or more elements of M are changed
- one or more elements are added to M
- one or more elements are removed from M
The naive approach of calculating S by iterating over the set is in O(n) time and O(1) space.
Storing all n subsets of M with n-1 elements results in O(1) time and O(n) space.
Id like a solution with O(log(n)) time and a good space complexity.
I thought about a sqrt(n)-tree which has average time and space complexities but requires annoying rebalancing.
Ideas?
Let S = m_1 * m_2 * m_3 * ... * m_n for m_i ∈ M.
I need a data structure for M that allows easy recalculation of S when:
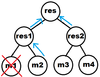
- one or more elements of M are changed
- one or more elements are added to M
- one or more elements are removed from M
The naive approach of calculating S by iterating over the set is in O(n) time and O(1) space.
Storing all n subsets of M with n-1 elements results in O(1) time and O(n) space.
Id like a solution with O(log(n)) time and a good space complexity.
I thought about a sqrt(n)-tree which has average time and space complexities but requires annoying rebalancing.
Ideas?