- Joined
- Aug 26, 2009
- Messages
- 192
Somehow the latex formulars aren't shown correctly, hence i added links.
Hey guys,
I'll just state my problem. I have a natural number n and I want to know if there exists a natural number m such that m^2 = n. Or in general, I have two natural numbers n, k and I want to know if there exists a natural numbers m such that m^k = n. The best would be if I could also obtain this natural number m. The most naive way would be just to try out the numbers. So we would have something like
Since the power can be calculated in logarithmic time and the loop goes till k-root(n) we have log(k) * k-root(n) operations. But these are multiplications hence a bit slower anyway. So i came up with another idea. For square numbers we have a cool formular! The sum of the first n odd numbers is n^2, hence
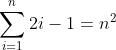
LaTeX1
Therefore we could just add them up and only have additions (except the one multiplication with 2). Hence the code would be something like
Here we have only 2 * sqrt(n) additions. In comparison, we had sqrt(n) * log(2) multiplications before.
So I tryed generalizing this and found the following formular:
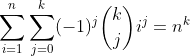
LaTeX2
Note that the proof shouldn't be that hard with induction and using the binomial theorem.
Well, as you can see, this needs fucking lots of operations.
While the inner power can be calculated quite fast by remembering the calculations, the binomial coefficient is slow. Anyway, these could just be calculated once and saved into an array. The (-1)^j could be exchanged by cases with calculating modulo, hence does not need log(j) time. Hence we come up with 2k multiplications and k additions/subtractions in the inner sum. Therefore we have 3k * k-root(n) + O(binomial coefficients) operations.
So it seems like this isn't the right way to look for a better algorithm or I just missed something.
So my question is: Do you know a better algorithm then just trying out the numbers from 1 to k-root(n) or do you have any ideas about my formulars?
That's all for now, thanks in advance!
Hey guys,
I'll just state my problem. I have a natural number n and I want to know if there exists a natural number m such that m^2 = n. Or in general, I have two natural numbers n, k and I want to know if there exists a natural numbers m such that m^k = n. The best would be if I could also obtain this natural number m. The most naive way would be just to try out the numbers. So we would have something like
Code:
for (int i = 0; x = pow(i,k) < n; ++i) {
if (x == n) {
return true;
}
}
return false;Since the power can be calculated in logarithmic time and the loop goes till k-root(n) we have log(k) * k-root(n) operations. But these are multiplications hence a bit slower anyway. So i came up with another idea. For square numbers we have a cool formular! The sum of the first n odd numbers is n^2, hence
LaTeX1
Therefore we could just add them up and only have additions (except the one multiplication with 2). Hence the code would be something like
Code:
int res = 0;
for (int i = 1; res < n; i +=2) {
res = res + i - 1;
if (res == n) {
return true;
}
}
return false;Here we have only 2 * sqrt(n) additions. In comparison, we had sqrt(n) * log(2) multiplications before.
So I tryed generalizing this and found the following formular:
LaTeX2
Note that the proof shouldn't be that hard with induction and using the binomial theorem.
Well, as you can see, this needs fucking lots of operations.
While the inner power can be calculated quite fast by remembering the calculations, the binomial coefficient is slow. Anyway, these could just be calculated once and saved into an array. The (-1)^j could be exchanged by cases with calculating modulo, hence does not need log(j) time. Hence we come up with 2k multiplications and k additions/subtractions in the inner sum. Therefore we have 3k * k-root(n) + O(binomial coefficients) operations.
So it seems like this isn't the right way to look for a better algorithm or I just missed something.
So my question is: Do you know a better algorithm then just trying out the numbers from 1 to k-root(n) or do you have any ideas about my formulars?
That's all for now, thanks in advance!
Last edited:



