- Joined
- Oct 11, 2018
- Messages
- 6
Introduction
Shared Income Mode is a feature used in many custom games: It causes each player in the game to receive the same amount of gold as the other players, regardless of how much gold that player himself earned.
However, maybe you do not want 100% of all income to be shared - that would be unfair! Perhaps you only want a percentage of all income to be shared as a way of lightly "rubber banding" players together, and keeping noobs from falling too far behind in the game. For example, in my map, Azure TD Remastered, I make it so that only 33% of each player's income is evenly distributed among allies.
The triggers to do this are actually pretty simple and versatile. I will show you a step-by-step process for creating a Shared Income system that only distributes a percentage of each player's income.
Step 1: Count Human Players
The first thing we need to do is create 2 variables: a Player Group variable that includes only Human, non-computer players, and an integer variable that keeps track of the number of Human players. The reason for this is because we may not want to include computer players in the Shared Income system. In melee games, computers earn gold differently than Human players, which can mess up the Shared Income system. In custom games, computers usually only exist as "dummy" players or players meant only to fill a game slot. We will want to exclude them from the Shared Income system. If you, by chance, have a working AI that you want to include into your Shared Income system, then feel free to add computer players into these variables as well:
-
 Count Human Players
Count Human Players
-
 Events
Events
-
 Map initialization
Map initialization
-
-

 Conditions
Conditions
-
 Actions
Actions
-


 Player Group - Pick every player in (All players) and do (Actions)
Player Group - Pick every player in (All players) and do (Actions)
-



 Loop - Actions
Loop - Actions
-




 If (All Conditions are True) then do (Then Actions) else do (Else Actions)
If (All Conditions are True) then do (Then Actions) else do (Else Actions)
-





 If - Conditions
If - Conditions
-




 ((Picked player) controller) Equal to User
((Picked player) controller) Equal to User
-
-





 Then - Actions
Then - Actions
-




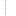

 Player Group - Add (Picked player) to ActiveHumanPlayers
Player Group - Add (Picked player) to ActiveHumanPlayers
-




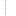
 Set ActiveHumanPlayerCount = (ActiveHumanPlayerCount + 1)
Set ActiveHumanPlayerCount = (ActiveHumanPlayerCount + 1)
-
-





 Else - Actions
Else - Actions
-





 Do nothing
Do nothing
-
-
-
-
-
-
Step 2: Create a Dummy "Distributor" Player
Our next step is to create a dummy player that will be our "distributor"; all the income that is to be distributed will be taxed to this player, and then this player will evenly distribute his received gold back to the other players.
We will do this by setting a gold threshold, that, when the dummy player's gold reaches this threshold, it distributes all its gold evenly back to each player. I recommend setting this threshold to a number that is low enough that it will provide constant income, but high enough that it can be divided among each player without creating rounding issues that will affect the total amount of gold flowing back out to players. In my map, which can have up to 8 players, I set this threshold to 50:
-
 Redistribute Income
Redistribute Income
-

 Events
Events
-
 Player - Player 12 (Brown)'s Current gold becomes Greater than or equal to 50.00
Player - Player 12 (Brown)'s Current gold becomes Greater than or equal to 50.00
-
-

 Conditions
Conditions
-

 Actions
Actions
-


 Set GoldToBeDistributed = ((Player 12 (Brown) Current gold) / ActiveHumanPlayerCount)
Set GoldToBeDistributed = ((Player 12 (Brown) Current gold) / ActiveHumanPlayerCount)
-


 Player Group - Pick every player in ActiveHumanPlayers and do (Actions)
Player Group - Pick every player in ActiveHumanPlayers and do (Actions)
-


 Loop - Actions
Loop - Actions
-


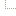
 Player - Add GoldToBeDistributed to (Picked player) Current gold
Player - Add GoldToBeDistributed to (Picked player) Current gold
-
-
-

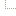
 Player - Set Player 12 (Brown) Current gold to 0
Player - Set Player 12 (Brown) Current gold to 0
-
-
Step 3: Tax each Player the % of Shared Income
However, in order for our "distributor" player to actually do anything, he will need to receive gold from the other players that he can evenly distribute back out. This is done through another trigger that we will use to divert a percentage of each player's income to our dummy player.
-
 Divert Income
Divert Income
-

 Events
Events
-

 Conditions
Conditions
-

 Actions
Actions
-


 Game - Display to (All players) the text: |c00FFFF00Shared In...
Game - Display to (All players) the text: |c00FFFF00Shared In...
-


 Player - Set Player 12 (Brown) Current gold to 25
Player - Set Player 12 (Brown) Current gold to 25
-


 Player Group - Pick every player in ActiveHumanPlayers and do (Actions)
Player Group - Pick every player in ActiveHumanPlayers and do (Actions)
-



 Loop - Actions
Loop - Actions
-



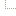
 Player - Divert 33% of the Gold income of (Picked player) to Player 12 (Brown)
Player - Divert 33% of the Gold income of (Picked player) to Player 12 (Brown)
-
-
-
-
The "33%" is the key number in this trigger - it specifies exactly how much of each player's income will end up being shared. You can change this number to something like 20%, 50%, or even go full-on communism and tax each player 100% of their income. You can even create a voting system that allows players to vote on what % of income may be shared, using a similar set of triggers to those found in this tutorial: Creating a Mode Voting System that averages Player Votes.
Bonus: Diverting Leaver Income
Another function of this trigger is that it can allow you to divert income from leavers to other players. You may not always want this feature - most games usually simply give full control of leavers and allow other players to spend the leaver's gold. However, in some custom games you may simply want the leaver's gold to be distributed out for other players to spend. To do this, simply make a trigger that diverts all of the leaver's current gold as well as his future income to our dummy "distributor" player.
-
 Give Leaver Gold and Control
Give Leaver Gold and Control
-

 Events
Events
-
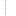

 Player - Player 1 (Red) leaves the game
Player - Player 1 (Red) leaves the game
-

 Player - Player 2 (Blue) leaves the game
Player - Player 2 (Blue) leaves the game
-

 Player - Player 3 (Teal) leaves the game
Player - Player 3 (Teal) leaves the game
-

 Player - Player 4 (Purple) leaves the game
Player - Player 4 (Purple) leaves the game
-

 Player - Player 5 (Yellow) leaves the game
Player - Player 5 (Yellow) leaves the game
-

 Player - Player 6 (Orange) leaves the game
Player - Player 6 (Orange) leaves the game
-

 Player - Player 7 (Green) leaves the game
Player - Player 7 (Green) leaves the game
-
 Player - Player 8 (Pink) leaves the game
Player - Player 8 (Pink) leaves the game
-
-

 Conditions
Conditions
-

 Actions
Actions
-


 Player Group - Remove (Triggering player) from ActiveHumanPlayers
Player Group - Remove (Triggering player) from ActiveHumanPlayers
-


 Set ActiveHumanPlayerCount = (ActiveHumanPlayerCount - 1)
Set ActiveHumanPlayerCount = (ActiveHumanPlayerCount - 1)
-


 Set LeaverGold = ((Triggering player) Current gold)
Set LeaverGold = ((Triggering player) Current gold)
-


 Player Group - Pick every player in ActiveHumanPlayers and do (Actions)
Player Group - Pick every player in ActiveHumanPlayers and do (Actions)
-


 Loop - Actions
Loop - Actions
-


 Player - Add (LeaverGold / ActiveHumanPlayerCount) to (Picked player) Current gold
Player - Add (LeaverGold / ActiveHumanPlayerCount) to (Picked player) Current gold
-
-
-


 Set LeaverGold = 0
Set LeaverGold = 0
-


 Player - Set (Triggering player) Current gold to 0
Player - Set (Triggering player) Current gold to 0
-


 Game - Grant shared vision and full shared unit control of (Triggering player) units with his/her allies
Game - Grant shared vision and full shared unit control of (Triggering player) units with his/her allies
-

 Player - Divert 100% of the Gold income of (Triggering player) to Player 12 (Brown)
Player - Divert 100% of the Gold income of (Triggering player) to Player 12 (Brown)
-
-
Conclusion
That concludes this tutorial on creating Shared Income modes. I hope that these triggers will be useful in future games and maps that you guys create!
-Eric Jensen [BYU_FOOTBALL]







