[Math; Calculus] Polar Planes

[indomitable1319]

Alright. I've started to grow an interest for these circles ever since I could make awesome effects with them using Daelin's awesome tutorial.

Now, I've borrowed some of my brother's Calculus notes, and saw something that was plotted on a Polar Plane that looked very interesting; it was a four-petaled rose.

Now, once I saw it; I immediately said: "Damn, I want to make that."
And so I did.

Here's what my brother's notes say:
Roses
A rose is a polar curve with equation:
r = (a(Cos(n(theta))))
Wherein:
a = Length of petal
n = Number of petals; if even then it becomes 2n
theta = Angle

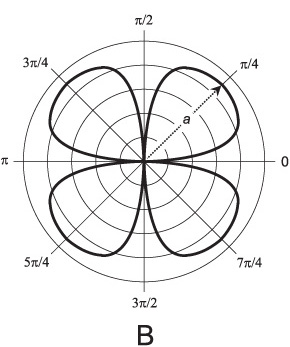
So here's one example.
r = (4(Cos(4(45 degrees))))
That makes a four-petaled rose with length 4.
4 points in all directions, and one petal each in of the four basic directions. It looks something like this:

Like this, except it should be pointing to the North, East, South and West and is less, 'puffy' than this one.

So, since I'm making that via triggers, I need to find out how to implement that.

First I tried setting the values into variables and doing it normally through triggering.
All it did was create a load of effects in one point.
And, I'm using the Special Effect - Create action to make this; and I am also using the Polar Plane with Offset function call.

Help will be greatly appreciated. Thank you.

 

[HINDYhat]

Do you understand what polar coordinates are? If so, you should understand this pretty quickly. If not, read the following spoiler:

Polar

In most (math) functions you've probably seen, you have one input (x) and one output (y). e.g. y = f(x) = x². This makes it really nice to draw on a grid, since x represents the distance from the Y axis, and y represents the distance from the X axis.

What if you wanted to represent a circle? Then, you'd use the implicit equation, x² + y² = r², which is readily understood if you think "(x, y) is a point on the circle if and only if x² + y² = r²." It's harder to draw, just by looking at the equation, because you don't have a one input, one output kind of thing, like you did for y = x².

So now, we have polar coordinates. Polar coordinates are like cartesian coordinates, except instead of working with (x, y) to specify a point, you work with (r, θ). r represents the distance from your point to the point (0, 0) on a grid, and θ represents counterclockwise angle from the positive X axis to your point. This is great, because now it's easy to draw circles and stuff in polar coodinates. A circle of radius R would be described with r = R, which is understood as "(r, θ) is a point on the circle if and only if r = R," which makes a lot of sense.

But you can get polar coordinate equations with one input and one output too. For example, r = θ. Then, you could say, for input angle θ, draw a point at (r, θ).

So, now that you know what polar coordinates are, and assuming you have basic knowledge of trigonometry, you should be able to figure out how to switch between polar and cartesian coordinates. Look at the following image:

This should be clear from basic trig. So now, you know that given (x, y), the polar coordinate form is:
r = sqrt(x² + y²) : the hypotenuse
θ = atan(y/x) : the angle between the positive X axis and (x, y). In Jass, use Atan2(y, x)

And given (r, θ), the cartesian coordinate form is:
x = r cos(θ)
y = r sin(θ)

What you want to do in your trigger is draw a rose. You have one input (θ) and one output (r). So here's the basic procedure:
1. Input θ, find r
2. Translate (r, θ) to (x, y)
3. Draw a special effect at (x, y)
4. Increment θ by a small amount
5. Rinse and repeat

You could probably use a silly GUI function like "point at distance from angle" or whatever, but that's silly, so don't.

 

[The Reborn Devil]

Basically,

θ ϵ [0, 2PI>
a = some length
n = some number
r = (a(Cos(n(θ))))
x = r Cos(θ)
y = r Sin(θ)

Example (The effect is deleted immediately after creation. If you want them to last, just edit this example and put the effects in an array):

• Derp
  • Events: No you
  • Conditions: No you
  • Actions:
    • Set Theta = 0
    • Set Increment = <some number, not too small and not too low. Perhaps something like 0.1>
    • Set Length = <some length>
    • Set Petals = <some number>
    • Set EffectModel = <some model>
    • Set CentreX = X coordinate of <some position>
    • Set CentreY = Y coordinate of <some position>
    • Custom script: loop
      • Custom script: exitwhen Theta >= 2*bj_PI
      • Set R = Length*(Cos(Petals*Theta))
      • Set X = CentreX + (R*Cos(Theta))
      • Set Y = CentreY + (R*Sin(Theta))
      • -------- Custom script FTW --------
      • Custom script: call DestroyEffect(AddSpecialEffect(udg_EffectModel, udg_X, udg_Y))
      • Set Theta = Theta + Increment
    • Custom script: endloop

I probably got something wrong here. I haven't completely woken up yet

 

[indomitable1319]

Do you understand what polar coordinates are? If so, you should understand this pretty quickly. If not, read the following spoiler:

Polar

In most (math) functions you've probably seen, you have one input (x) and one output (y). e.g. y = f(x) = x². This makes it really nice to draw on a grid, since x represents the distance from the Y axis, and y represents the distance from the X axis.

What if you wanted to represent a circle? Then, you'd use the implicit equation, x² + y² = r², which is readily understood if you think "(x, y) is a point on the circle if and only if x² + y² = r²." It's harder to draw, just by looking at the equation, because you don't have a one input, one output kind of thing, like you did for y = x².

So now, we have polar coordinates. Polar coordinates are like cartesian coordinates, except instead of working with (x, y) to specify a point, you work with (r, θ). r represents the distance from your point to the point (0, 0) on a grid, and θ represents counterclockwise angle from the positive X axis to your point. This is great, because now it's easy to draw circles and stuff in polar coodinates. A circle of radius R would be described with r = R, which is understood as "(r, θ) is a point on the circle if and only if r = R," which makes a lot of sense.

But you can get polar coordinate equations with one input and one output too. For example, r = θ. Then, you could say, for input angle θ, draw a point at (r, θ).

So, now that you know what polar coordinates are, and assuming you have basic knowledge of trigonometry, you should be able to figure out how to switch between polar and cartesian coordinates. Look at the following image:

This should be clear from basic trig. So now, you know that given (x, y), the polar coordinate form is:
r = sqrt(x² + y²) : the hypotenuse
θ = atan(y/x) : the angle between the positive X axis and (x, y). In Jass, use Atan2(y, x)

And given (r, θ), the cartesian coordinate form is:
x = r cos(θ)
y = r sin(θ)

What you want to do in your trigger is draw a rose. You have one input (θ) and one output (r). So here's the basic procedure:
1. Input θ, find r
2. Translate (r, θ) to (x, y)
3. Draw a special effect at (x, y)
4. Increment θ by a small amount
5. Rinse and repeat

You could probably use a silly GUI function like "point at distance from angle" or whatever, but that's silly, so don't.

Nope, I don't have basic knowledge of Trigonometry.
So, I'll just keep reading this over and over again until I fully understand.

Basically,

θ ϵ [0, 2PI>
a = some length
n = some number
r = (a(Cos(n(θ))))
x = r Cos(θ)
y = r Sin(θ)

Example (The effect is deleted immediately after creation. If you want them to last, just edit this example and put the effects in an array):

• Derp
  • Events: No you
  • Conditions: No you
  • Actions:
    • Set Theta = 0
    • Set Increment = <some number, not too small and not too low. Perhaps something like 0.1>
    • Set Length = <some length>
    • Set Petals = <some number>
    • Set EffectModel = <some model>
    • Set CentreX = X coordinate of <some position>
    • Set CentreY = Y coordinate of <some position>
    • Custom script: loop
      • Custom script: exitwhen Theta >= 2*bj_PI
      • Set R = Length*(Cos(Petals*Theta))
      • Set X = CentreX + (R*Cos(Theta))
      • Set Y = CentreY + (R*Sin(Theta))
      • -------- Custom script FTW --------
      • Custom script: call DestroyEffect(AddSpecialEffect(udg_EffectModel, udg_X, udg_Y))
      • Set Theta = Theta + Increment
    • Custom script: endloop

I probably got something wrong here. I haven't completely woken up yet

What kind of Variable is EffectModel?
Also, CentreX and CentreY: I'm not too sure on how to implement this since I want the effect to be created around the unit that triggers the event.

[EDIT]
Alright, I've made the trigger, but I still don't know what kind of variable EffectModel is, and how to set CentreX and CentreY up when I want it to run where the caster is.
Obviously, it doesn't work.

My Trigger

• (Ability Name)
  • Events
    • Unit - A unit Starts the effect of an ability
  • Conditions
    • (Ability being cast) Equal to (Ability)
  • Actions
    • Set Caster = (Casting unit)
    • Set CasterPoint = (Position of Caster)
    • Set Theta = 0.00
    • Set Increment = 0.10
    • Set Length = 500.00
    • Set Petals = 4
    • Set EffectModel = Human Crater
    • Custom script: loop
    • Custom script: exitwhen Theta >= 2*bj_PI
    • Set R = (Length x (Cos(((Real(Petals)) x Theta))))
    • Set X = ((Real(CentreX)) + (R x (Cos(Theta))))
    • Set Y = ((Real(CentreY)) + (R x (Sin(Theta))))
    • Custom script: call DestroyEffect(AddSpecialEffect(udg_EffectModel, udg_X, udg_Y))
    • Set Theta = (Theta + Increment)
    • Custom script: endloop

Also, when it saves, it says that:

• Custom script: exitwhen Theta >= 2*bj_PI

Is causing some problems, and it ended up making me turn the trigger off.

 

[The Reborn Devil]

Oh yes, the error is because I forgot "udg_" in front of Theta
I'm so used to regular JASS where the udg_ isn't needed.

EffectModel is a string. It's the path to the model you want to use.
For instance, lets say you did this in GUI:

• Special Effect - Create a special effect at (Center of (Playable map area)) using Abilities\Spells\Human\ThunderClap\ThunderClapCaster.mdl

The effect model is "Abilities\Spells\Human\ThunderClap\ThunderClapCaster.mdl" (without quotation marks).

CentreX and CentreY is the x/y coordinates of the location of where you want the centre to be. If a unit is supposed to be in the centre then just use custom script.
Like this:

• Set Caster= <Your unit>
• Custom script: set udg_CentreX = GetUnitX(udg_Caster)
• Custom script: set udg_CentreY = GetUnitY(udg_Caster)

It's better to deal with coordinates than locations, because it's more efficient and there's no need to destroy them or null them, like you have to do with point variables.

 

[indomitable1319]

Ah, I see.
I'm quite new to the use of strings in that kind of way. I see.

CentreX and CentreY are what kind of variables? Reals?
Right now I'm using Integers, but I should switch to Reals.
Trying it now...

Here's what happened. When I cast the spell, the effect spawns only in the position of the caster.

Triggaaaaaaah.

• Weeee
  • Events
    • Unit - A unit Starts the effect of an ability
  • Conditions
    • (Ability being cast) Equal to (Ability)
  • Actions
    • Set Caster = (Casting unit)
    • Set CasterPoint = (Position of Caster)
    • Set Theta = 0.00
    • Set Increment = 0.10
    • Set Length = 500.00
    • Set Petals = 4
    • Set EffectModel = Abilities\Spells\Human\ThunderClap\ThunderClapCaster.mdl
    • Custom script: set udg_CentreX = GetUnitX(udg_Caster)
    • Custom script: set udg_CentreY = GetUnitY(udg_Caster)
    • Custom script: loop
    • Custom script: exitwhen udg_Theta >= 2*bj_PI
    • Set R = (Length x (Cos(((Real(Petals)) x Theta))))
    • Custom script: call DestroyEffect(AddSpecialEffect(udg_EffectModel, udg_CentreX, udg_CentreY))
    • Set Theta = (Theta + Increment)
    • Custom script: endloop

 

[The Reborn Devil]

It only spawns in the centre because you're giving the CentreX and CentreY variables to the AddSpecialEffect function.
You're missing the X and Y variables which are the ones you are supposed to give to it.

Look at my code again:

• Set R = Length*(Cos(Petals*Theta))
• Set X = CentreX + (R*Cos(Theta))
• Set Y = CentreY + (R*Sin(Theta))
• -------- Custom script FTW --------
• Custom script: call DestroyEffect(AddSpecialEffect(udg_EffectModel, udg_X, udg_Y))

Now look at yours:

• Set R = (Length x (Cos(((Real(Petals)) x Theta))))
• Custom script: call DestroyEffect(AddSpecialEffect(udg_EffectModel, udg_CentreX, udg_CentreY))

Do you see the difference (besides the differences in signs/parenthesis) ?

Edit: CentreX, CentreY, X and Y are reals.

 

[indomitable1319]

Oh, I see.
I fail.
Alright, wait.
I removed:

• Custom script: exitwhen udg_Theta >= 2*bj_PI

And it worked, but with such lag. Good thing my computer can take it.

Here's the attachment. I used the Death Coil art.

This is my current trigger.

Once again.

• Roseeeee
  • Events
    • Unit - A unit Starts the effect of an ability
  • Conditions
    • (Ability being cast) Equal to (Ability)
  • Actions
    • Set Caster = (Casting unit)
    • Set CasterPoint = (Position of Caster)
    • Set Theta = 0.00
    • Set Increment = 0.10
    • Set Length = 1000.00
    • Set Petals = 4
    • Set EffectModel = Abilities\Spells\Undead\DeathCoil\DeathCoilSpecialArt.mdl
    • Custom script: set udg_CentreX = GetUnitX(udg_Caster)
    • Custom script: set udg_CentreY = GetUnitY(udg_Caster)
    • Custom script: loop
    • Set R = (Length x (Cos(((Real(Petals)) x Theta))))
    • Set X = (CentreX + (R x (Cos(Theta))))
    • Set Y = (CentreY + (R x (Sin(Theta))))
    • Custom script: call DestroyEffect(AddSpecialEffect(udg_EffectModel, udg_X, udg_Y))
    • Set Theta = (Theta + Increment)
    • Custom script: endloop

[EDIT]
I can't seem to upload the picture right now.

[EDIT 2]
Alright. I can upload the picture now.
I have a question though, how could I make it less laggy?
Please, don't mind the pictures' names.

 

[HINDYhat]

I have a question though, how could I make it less laggy?

Removing that line means the trigger loops indefinitely, which means a shitton of lag and probably an op limit at some point. Basically, leave that line in, but make your Increment smaller.

 

[indomitable1319]

Alright, I'll place it back in.
Smaller? .1 is my current value, I'll try changing it to .02 or something.

[EDIT]
I put the Custom Script back in the original trigger, but it doesn't create the entire rose.

 

[HINDYhat]

Make your Increment smaller, or try changing udg_Theta >= 2*bj_PI to like udg_Theta >= 10*bj_PI or something.

 

[indomitable1319]

I'll try changing the 2*bj_PI into something higher.

 

[HINDYhat]

The factor should be an even number btw. I mean,
4*bj_PI, 6*bj_PI, 8*bj_PI etc. are all good.
3*bj_PI, 5*bj_PI, etc. are bad.

 

[indomitable1319]

Ah, I see.
Alright, thanks.