- Joined
- Mar 27, 2008
- Messages
- 8,035
I need to move my unit in elliptical manner, here's a picture which will explain it further how the movement is done.
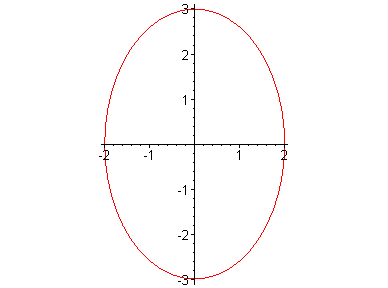
Is there any useful formula/method to execute this kind of movement ?
Example:
Initially, my unit is at -3 y-axis.
When I cast a spell targeting at +3 y-axis, my unit will move from -3 y-axis > +2 x-axis > -3 y-axis > -2 x-axis > -3 y-axis.
It seems like it goes into full complete circle, but it's not a circle, it's an ellipse.
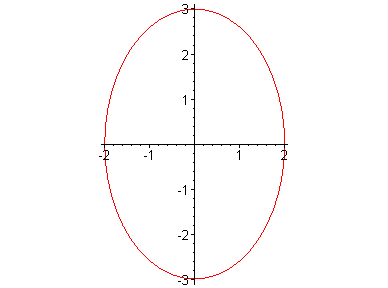
Is there any useful formula/method to execute this kind of movement ?
Example:
Initially, my unit is at -3 y-axis.
When I cast a spell targeting at +3 y-axis, my unit will move from -3 y-axis > +2 x-axis > -3 y-axis > -2 x-axis > -3 y-axis.
It seems like it goes into full complete circle, but it's not a circle, it's an ellipse.




