Community
Maps
Tutorials
Gallery
Support Us
Install the app
-
Listen to a special audio message from Bill Roper to the Hive Workshop community (Bill is a former Vice President of Blizzard Entertainment, Producer, Designer, Musician, Voice Actor) 🔗Click here to hear his message!
-
Read Evilhog's interview with Gregory Alper, the original composer of the music for WarCraft: Orcs & Humans 🔗Click here to read the full interview.
-
Create a faction for Warcraft 3 and enter Hive's 19th Techtree Contest: Co-Op Commanders! Click here to enter!
-
Create a void inspired texture for Warcraft 3 and enter Hive's 34th Texturing Contest: Void! Click here to enter!
-
The Hive's 21st Texturing Contest: Upgrade is now concluded, time to vote for your favourite set of icons! Click here to vote!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Fun math paradoxes, problems, and stuff
- Status
- Not open for further replies.
- Joined
- Feb 4, 2009
- Messages
- 1,314
got it down to
n^2 = product of 2-2*cos(x*2*pi/n) with x from 1 to n-1
this might be solved further but I don't know how so now it's up to someone else
(there probably is a trick to get rid of that cosine because in our case it does not cover all numbers but only multiples of 2*pi/n)
I guess replacing the cosine with its taylor series + proof by induction does not work because it would require 2 proofs with 1 formula or something but I didn't try that one yet
here is a proof to show that it also works for n = 100
http://www.wolframalpha.com/input/?i=product+2-2cos%28x*2*pi%2F100%29+from+1+to+99
n^2 = product of 2-2*cos(x*2*pi/n) with x from 1 to n-1
this might be solved further but I don't know how so now it's up to someone else
(there probably is a trick to get rid of that cosine because in our case it does not cover all numbers but only multiples of 2*pi/n)
I guess replacing the cosine with its taylor series + proof by induction does not work because it would require 2 proofs with 1 formula or something but I didn't try that one yet
here is a proof to show that it also works for n = 100
http://www.wolframalpha.com/input/?i=product+2-2cos%28x*2*pi%2F100%29+from+1+to+99
- Joined
- Apr 22, 2007
- Messages
- 1,960
I'll help because I haven't solved it either, but I feel devilishly close.
The kth segment I've found is 2sin(kπ/n). So, you need to show that:
n = 2sin(1π/n) * 2sin(2π/n) * ... * 2sin((n-1)π/n)
You can simplify this product further by converting sin to its complex equivalent, that is:
sin(x) = (eiπx - e-iπx)/2i, which gives:
n = (1 - γ-1) * (1 - γ-2) * ... * (1 - γ-(n-1))
where γ = e2πi/n
I recieved a tip here that I should try to find an expression for:
f(z) = (z - γ-1) * (z - γ-2) * ... * (z - γ-(n-1))
and then evaluate f(1). Also, to find f(z), I should try multiplying by (z - 1)/(z - 1). I tried this, and I've come to realize that in all cases I've carried out,
(z - 1) * (z - γ-1) * (z - γ-2) * ... * (z - γ-(n-1)) / (z - 1)
= (zn - 1) / (z - 1) = zn-1 + zn -2 + ... + z + 1
Which is great, because then f(1) = n. However, I don't know how to prove this. So far, what I've got is:
We want to show that (z - 1) * (z - γ-1) * (z - γ-2) * ... * (z - γ-(n-1)) = zn - 1. The zn term obviously has coefficient 1. The z0 term can be shown to have coefficient -1 (this isn't so bad). All you have to do is show that every other term has coefficient 0. gl hf.
The kth segment I've found is 2sin(kπ/n). So, you need to show that:
n = 2sin(1π/n) * 2sin(2π/n) * ... * 2sin((n-1)π/n)
You can simplify this product further by converting sin to its complex equivalent, that is:
sin(x) = (eiπx - e-iπx)/2i, which gives:
n = (1 - γ-1) * (1 - γ-2) * ... * (1 - γ-(n-1))
where γ = e2πi/n
I recieved a tip here that I should try to find an expression for:
f(z) = (z - γ-1) * (z - γ-2) * ... * (z - γ-(n-1))
and then evaluate f(1). Also, to find f(z), I should try multiplying by (z - 1)/(z - 1). I tried this, and I've come to realize that in all cases I've carried out,
(z - 1) * (z - γ-1) * (z - γ-2) * ... * (z - γ-(n-1)) / (z - 1)
= (zn - 1) / (z - 1) = zn-1 + zn -2 + ... + z + 1
Which is great, because then f(1) = n. However, I don't know how to prove this. So far, what I've got is:
We want to show that (z - 1) * (z - γ-1) * (z - γ-2) * ... * (z - γ-(n-1)) = zn - 1. The zn term obviously has coefficient 1. The z0 term can be shown to have coefficient -1 (this isn't so bad). All you have to do is show that every other term has coefficient 0. gl hf.
- Joined
- Feb 4, 2009
- Messages
- 1,314
You can simplify this product further by converting sin to its complex equivalent, that is:
sin(x) = (eiπx - e-iπx)/2i
simplify?
complex numbers?

- Joined
- Apr 22, 2007
- Messages
- 1,960
simplify?
complex numbers?

It's a lot simpler than the alternative, i.e. now it's possible.
- Joined
- Apr 22, 2007
- Messages
- 1,960
Proof!
Looking at the following:
(z - 1) * (z - γ-1) * (z - γ-2) * ... * (z - γ-(n-1))
This polynomial has, as roots, the primitive nth roots of unity. Thus, by definition:
(z - 1) * (z - γ-1) * (z - γ-2) * ... * (z - γ-(n-1)) = zn - 1
So:
f(z) = (zn - 1)/(z - 1) = zn-1 + zn-2 + ... + z + 1,
which means that f(1) = n.
Q.E.D.
FUCK YEAH. I'll update this with the complete proof once I'm not at work lolo.
Looking at the following:
(z - 1) * (z - γ-1) * (z - γ-2) * ... * (z - γ-(n-1))
This polynomial has, as roots, the primitive nth roots of unity. Thus, by definition:
(z - 1) * (z - γ-1) * (z - γ-2) * ... * (z - γ-(n-1)) = zn - 1
So:
f(z) = (zn - 1)/(z - 1) = zn-1 + zn-2 + ... + z + 1,
which means that f(1) = n.
Q.E.D.
FUCK YEAH. I'll update this with the complete proof once I'm not at work lolo.
Last edited:
- Joined
- Apr 22, 2007
- Messages
- 1,960
ALRIGHT FULL PROOF BITCHES. Also, triple post because I feel like it and also to bump this awesome occasion!
Some theory to preamble this proof.
An nth root of unity is a complex number z that satisfies the equation zn = 1, i.e. that is a root of the polynomial zn - 1.
One can show that the nth roots of unity are e2πi k/n, where k ranges from 0 to n-1.
It should be clear from Euler's formula, eix = cos x + i sin x, that the nth primitive roots of unity describe vertices of a regular n-gon inscribed in a circle of radius 1 in the complex plane:
e2πi k/n = cos(2πk/n) + i sin(2πk/n)
So the vertex is, in polar coordinates, at (1, 2π k/n). This should make it pretty obvious.
We will denote ɣ = e2πi/n. In this way, ɣk is the primitive kth root of unity. Then, the distance between the vertex (1, 0), and the kth vertex in the inscribed n-gon is:
sqrt((Re(ɣk) - 1)2 + Im(ɣk)2)
= sqrt(2 - 2cos(2πk/n)) = 2sin(πk/n)
Then, we're trying to show that
n = 2sin(π 1/n) * 2sin(π 2/n) * ... * 2sin(π (n-1)/n)
Convert sin to its complex exponential equivalent, and we can simplify this product to the following:
n = (1 - ɣ-1) * ((1 - ɣ-2) * ... * (1 - ɣ-(n-1))
Consider the function f,
f(z) = (z - 1) * (z - ɣ-1) * ((z - ɣ-2) * ... * (z - ɣ-(n-1))
f is a polynomial, and its roots are the nth roots of unity (of multiplicity 1). Thus, by definition, f(z) = zn - 1.
Then, f(z)/(z - 1) = (zn - 1)/(z - 1) = zn-1 + zn-2 + ... + z + 1 = g(z)
Since g(1) = n, we are done. Q.E.D.
FUCK YEAH.
Some theory to preamble this proof.
An nth root of unity is a complex number z that satisfies the equation zn = 1, i.e. that is a root of the polynomial zn - 1.
One can show that the nth roots of unity are e2πi k/n, where k ranges from 0 to n-1.
It should be clear from Euler's formula, eix = cos x + i sin x, that the nth primitive roots of unity describe vertices of a regular n-gon inscribed in a circle of radius 1 in the complex plane:
e2πi k/n = cos(2πk/n) + i sin(2πk/n)
So the vertex is, in polar coordinates, at (1, 2π k/n). This should make it pretty obvious.
We will denote ɣ = e2πi/n. In this way, ɣk is the primitive kth root of unity. Then, the distance between the vertex (1, 0), and the kth vertex in the inscribed n-gon is:
sqrt((Re(ɣk) - 1)2 + Im(ɣk)2)
= sqrt(2 - 2cos(2πk/n)) = 2sin(πk/n)
Then, we're trying to show that
n = 2sin(π 1/n) * 2sin(π 2/n) * ... * 2sin(π (n-1)/n)
Convert sin to its complex exponential equivalent, and we can simplify this product to the following:
n = (1 - ɣ-1) * ((1 - ɣ-2) * ... * (1 - ɣ-(n-1))
Consider the function f,
f(z) = (z - 1) * (z - ɣ-1) * ((z - ɣ-2) * ... * (z - ɣ-(n-1))
f is a polynomial, and its roots are the nth roots of unity (of multiplicity 1). Thus, by definition, f(z) = zn - 1.
Then, f(z)/(z - 1) = (zn - 1)/(z - 1) = zn-1 + zn-2 + ... + z + 1 = g(z)
Since g(1) = n, we are done. Q.E.D.
FUCK YEAH.
- Joined
- Dec 12, 2008
- Messages
- 7,385
@HINDYhat:
Awww... You beat me to it
Awww... You beat me to it
- Joined
- Apr 3, 2010
- Messages
- 1,101
ALRIGHT FULL PROOF BITCHES. Also, triple post because I feel like it and also to bump this awesome occasion!
Since g(1) = n, we are done. Q.E.D.
FUCK YEAH.
Math high?
Nice solving i understood 1% of that solution but im a maths retard so hec.
Here a problem for you guys.
There is a square house. Each side of the house has a window> And there are 8 fields surrounding the house. It is so you can see 3 fields through each window.
Through each window you can see the same amount of sheep.
Yet there is a total of 46 Sheep.
How many sheep are on each field?
FIELD A FIELD B FIELD C
FIELD D HOUSE! FIELD E
FIELD F FIELD G FIELD H
Edit: kk tyx below fixed the number,.
Last edited:
- Joined
- Jun 16, 2011
- Messages
- 45
There are 8 fields, not 9. Also, do I have to calculate number of sheep on every field?
- Joined
- Apr 22, 2007
- Messages
- 1,960
Without having calculated anything, I can already tell that the fields can have varying amounts of sheep. Only A = C = F = H, and B = D = E = G, and there is a linear relationship between the diagonal fields and the horizontal/vertical fields.
- Joined
- Jun 16, 2011
- Messages
- 45
Without having calculated anything, I can already tell that the fields can have varying amounts of sheep. Only A = C = F = H, and B = D = E = G, and there is a linear relationship between the diagonal fields and the horizontal/vertical fields.
How comes that? If I can see the same amount of sheep from every window then it's A+B+C=A+D+F=F+G+H=C+E+H and A+B+C+D+E+F+G+H=46.
- Joined
- Apr 22, 2007
- Messages
- 1,960
Those are valid of course. There are a ton of equations that you have to consider for this kind of problem. The point is, nowhere is it stated that the number of sheep in every field is the same. Thus, the corner fields can have differing counts from the non-corner fields, since when you look out a window, you don't see a field. You see two corner fields and one non-corner field.
If you can't understand this intuitively, I suggest you solve it mathematically. It's pretty easy to solve using a system of equations and matrices and such. There's probably a simpler way but I don't really care.
If you can't understand this intuitively, I suggest you solve it mathematically. It's pretty easy to solve using a system of equations and matrices and such. There's probably a simpler way but I don't really care.
- Joined
- Jul 6, 2009
- Messages
- 1,885
That would mean A+B=C+E=H+G=F+D in which case the amount of sheep would be divisible by 4 and it isn't.Without having calculated anything, I can already tell that the fields can have varying amounts of sheep. Only A = C = F = H, and B = D = E = G, and there is a linear relationship between the diagonal fields and the horizontal/vertical fields.
- Joined
- Apr 22, 2007
- Messages
- 1,960
That would mean A+B=C+E=H+G=F+D in which case the amount of sheep would be divisible by 4 and it isn't.
Hah, that's clever. Well then, there's a fucked up amount of sheep.
- Joined
- Dec 12, 2008
- Messages
- 7,385
Hah, that's clever. Well then, there's a fucked up amount of sheep
Divide them by 0.
Now you can call that value fucked up ;D
edit
What if some of the sheep were cut up
there could be half a sheep on every field xD
- Joined
- Jun 16, 2011
- Messages
- 45
What if some of the sheep were cut up
there could be half a sheep on every field xD
Exactly my thoughts.
fladdermasken
Off-Topic Moderator
- Joined
- Dec 27, 2006
- Messages
- 3,690
The riddle is inherently lacking awesomeness.
A(3) B(6) C(8) D(6) E(6) F(8) G(6) H(3) - ABC=ADF=FGH=CEH=17 - A+B+C+D+E+F+G+H=46
A(4) B(6) C(7) D(6) E(6) F(7) G(6) H(4) - ABC=ADF=FGH=CEH=17 - A+B+C+D+E+F+G+H=46
So yeah...
A(3) B(6) C(8) D(6) E(6) F(8) G(6) H(3) - ABC=ADF=FGH=CEH=17 - A+B+C+D+E+F+G+H=46
A(4) B(6) C(7) D(6) E(6) F(7) G(6) H(4) - ABC=ADF=FGH=CEH=17 - A+B+C+D+E+F+G+H=46
So yeah...
Without having calculated anything, I can already tell that the fields can have varying amounts of sheep.
- Joined
- Apr 22, 2007
- Messages
- 1,960
The riddle is inherently flawed in the sense that there are multiple answers.
A(3) B(6) C(8) D(6) E(6) F(8) G(6) H(3) - ABC=ADF=FGH=CEH=17 - A+B+C+D+E+F+G+H=46
A(4) B(6) C(7) D(6) E(6) F(7) G(6) H(4) - ABC=ADF=FGH=CEH=17 - A+B+C+D+E+F+G+H=46
So yeah...
Well then I guess I was right? Now I feel kind of silly haha.
fladdermasken
Off-Topic Moderator
- Joined
- Dec 27, 2006
- Messages
- 3,690
Your first intuition is usually right, I've royally messed up several exams by overanalyzing the simplest of shit :3Well then I guess I was right? Now I feel kind of silly haha.
- Joined
- Apr 22, 2007
- Messages
- 1,960
Here's a cool problem I found while browsing xkcd:
So, let's say you are prisoner of an evil dictator, which will give you a chance to give you back your freedom if you win at this little game :
He has put 100 boxes in a room, and every box has a number from 1 to 100. Additionally, each box contains a card with a number between 1 and 100. Those numbers are chosen randomly, several boxes can contain cards with the same number.
When you enter the room, you have to chose one box, and open it. If the card it contains has the same number as the box itself, then you win. If it does not, then you are allowed to open the box with the same number as the card you just found, provided it still has not been opened. You can open as many boxes as you need to, the game stops when the number on the card is the same as the one on the box that contained it (you win), or when the number on the card matches a box that has already been opened (you lose).
Short example : You chose box 10, it contains card 20. You open box 20, it contains card 20, you win.
You chose box 10, it contains card 20. You open box 20, it contains card 10, box 10 has already been opened, you lose.
So, it is obviously not a question of strategy, the question is to determine the winning probability.
Here's a solution since nobody cares, shamelessly copied from xkcd.
Let's call the number of boxes already opened n, and the chance of winning eventually f(n).
You have a 1/100 chance of winning instantly.
You have a n/100 chance of losing instantly.
You have a (99 - n)/100 chance of continuing the game.
f(n) = 1/100 + (99 - n)/100 * f(n + 1)
f(99) = 1/100
f(98) = 1/100 + 1/10000
f(97) = 1/100 + 2f(98)/100
f(96) = 1/100 + 3f(97)/100
f(95) = 1/100 + 4f(96)/100
...
*fiddles with formulas in Excel*
f(0) = 0.122099606 (approximately)
I don't think there's a good convenient way to give an explicit direct formula for it, you just have to go through the calculations.
So, you have a slightly less than 1/8 chance of winning.
fladdermasken
Off-Topic Moderator
- Joined
- Dec 27, 2006
- Messages
- 3,690
Anyone looking to prove their mettle, design a postulate for electron energy levels accounting for multiple-electron systems (such as for instance lithium)
I win at difficult tasks kthx?
I win at difficult tasks kthx?
Deleted member 177737
D
Deleted member 177737
Stop it...the math...it hurts!
- Joined
- Apr 22, 2007
- Messages
- 1,960
Anyone looking to prove their mettle, design a postulate for electron energy levels accounting for multiple-electron systems (such as for instance lithium)
I win at difficult tasks kthx?
Solve Hilbert's problems. gg
Stop it...the math...it hurts!
That's because Americans don't put an S on the end. The S makes it soft.
Mathsssss...
- Joined
- Apr 22, 2007
- Messages
- 1,960
Math high?
Nice solving i understood 1% of that solution but im a maths retard so hec.
Here a problem for you guys.
There is a square house. Each side of the house has a window> And there are 9 fields surrounding the house. It is so you can see 3 fields through each window.
Through each window you can see the same amount of sheep.
Yet there is a total of 46 Sheep.
How many sheep are on each field?
FIELD A FIELD B FIELD C
FIELD D HOUSE! FIELD E
FIELD F FIELD G FIELD H
I was bored so I decided to solve this right now. Based on the constraints you've listed, you have 5 equations and 9 unknowns (A, B, C, D, E, F, G, H, and x, where x is the number of sheep you see). I get:
A free choice on E, G, H and x.
A = E + G + H + 2x - 46
B = -G - 2x + 46
C = -E - H + x
D = -E - 2x + 46
F = -G - H + x
So, using this, I'll construct one of fladder's answers:
fladdermasken said:A(3) B(6) C(8) D(6) E(6) F(8) G(6) H(3) - ABC=ADF=FGH=CEH=17 - A+B+C+D+E+F+G+H=46
If we choose E = 6, G = 6, H = 3, x = 17, then:
A = 6 + 6 + 3 + 2*17 - 46 = 3
B = -6 - 2*17 + 46 = 6
C = -6 - 3 + 17 = 8
D = -6 - 2*17 + 46 = 6
E = 6
F = -6 - 3 + 17 = 8
G = 6
H = 3
So yeah, it seems to work. If I'm really bored, I'll count the total number of possible answers.
Deleted member 177737
D
Deleted member 177737
That's because Americans don't put an S on the end. The S makes it soft.
Mathsssss...
<----Canadian.
- Joined
- Apr 22, 2007
- Messages
- 1,960
This one is interesting, for those who have never taken an analysis class. It's to show that the 'size' of the set of rational numbers is the same as the size of the set of natural numbers.
To show that two sets of objects have the same size, you have to find a way of associating, for each object in the first set a unique object in the second set, and for each object in the second set a unique object in the first. For example, the set {apple, orange} has the same size as the set {1, 2}, since we associate apple with 1, and orange with 2. If we're given 1, we also know that we're talking about apples, and if we're given 2, we know that we're talking about oranges. It works both ways.
The set of rational numbers is the set of fractions, i.e. the set of numbers of the form a/b where a and b are natural numbers. For this problem, we're trying to show that the size of the set of natural numbers is the same as the size of the set of rationals. Some dude named Georg Cantor came up with a pretty badass argument for this. Consider the following diagram:

Each column increases the denominator by 1, and each row increases the numerator by 1. Starting from 1/1, the path of arrows traces the enumeration of rational numbers, so we can go through all rational numbers by following that path. Skip all the red fractions, since they can be simplified to previously enumerated fractions. So we have an enumeration of rational numbers (i.e. an association with natural numbers) as follows:
1: 1/1
2: 2/1
3: 1/2
4: 1/3
5: 3/1
6: 4/1
7: 3/2
8: 2/3
etc.
So, informally, there's a way of associating, for every natural number a unique rational number, and for every rational number a unique natural number. Thus, the sets must have the same size! Of course, this can be done formally as well, but that would be needlessly tiresome since you should get the jist of it anyway.
If this is the first time you've seen this, you should be questioning your existence right now.
To show that two sets of objects have the same size, you have to find a way of associating, for each object in the first set a unique object in the second set, and for each object in the second set a unique object in the first. For example, the set {apple, orange} has the same size as the set {1, 2}, since we associate apple with 1, and orange with 2. If we're given 1, we also know that we're talking about apples, and if we're given 2, we know that we're talking about oranges. It works both ways.
The set of rational numbers is the set of fractions, i.e. the set of numbers of the form a/b where a and b are natural numbers. For this problem, we're trying to show that the size of the set of natural numbers is the same as the size of the set of rationals. Some dude named Georg Cantor came up with a pretty badass argument for this. Consider the following diagram:

Each column increases the denominator by 1, and each row increases the numerator by 1. Starting from 1/1, the path of arrows traces the enumeration of rational numbers, so we can go through all rational numbers by following that path. Skip all the red fractions, since they can be simplified to previously enumerated fractions. So we have an enumeration of rational numbers (i.e. an association with natural numbers) as follows:
1: 1/1
2: 2/1
3: 1/2
4: 1/3
5: 3/1
6: 4/1
7: 3/2
8: 2/3
etc.
So, informally, there's a way of associating, for every natural number a unique rational number, and for every rational number a unique natural number. Thus, the sets must have the same size! Of course, this can be done formally as well, but that would be needlessly tiresome since you should get the jist of it anyway.
If this is the first time you've seen this, you should be questioning your existence right now.
<----Canadian.
Well yeah... you use the American spelling. And you're in the continent of (North) America, so I'm close enough.
- Joined
- Dec 12, 2008
- Messages
- 7,385
if:
f(0) = -4
f(1) = -2
f(2) = 8
f(3) = 48
Find f(x).
f(0) = -4
f(1) = -2
f(2) = 8
f(3) = 48
Find f(x).
- Joined
- Apr 3, 2010
- Messages
- 1,101
f(n)=(n-1)^2-n^2
Basically its like this
(1-Ans)^2-ANs^2=Y
So
Here is an example
(1-3)^2-Ans^2=-5
(1--5)^2--5^2=11
(1-11)^2-11^2=-21
Etc
The following is a list of the sequence (read downwards)
3 -1365 699051 -357914000 -1.466x10^12
-5 2731 -1398101 715828000 2.93x10^12
11 -5461 2796203 -1.14532x10^10 5.86x10^12
-21 10923 -5592405 -2.2907x10^10 1.17x10^13
43 -21845 11184811 4.5814x10^10 0
-85 43691 -22369621 -9.163x10^10 1
171 -87381 44738243 1.8326x10^10 -1
-341 174763 -89478480 -3.666x10^10 3
683 -349525 178956960 7.33x10^11 End of loop
So why does it loop back to 3 again?
r
Basically its like this
(1-Ans)^2-ANs^2=Y
So
Here is an example
(1-3)^2-Ans^2=-5
(1--5)^2--5^2=11
(1-11)^2-11^2=-21
Etc
The following is a list of the sequence (read downwards)
3 -1365 699051 -357914000 -1.466x10^12
-5 2731 -1398101 715828000 2.93x10^12
11 -5461 2796203 -1.14532x10^10 5.86x10^12
-21 10923 -5592405 -2.2907x10^10 1.17x10^13
43 -21845 11184811 4.5814x10^10 0
-85 43691 -22369621 -9.163x10^10 1
171 -87381 44738243 1.8326x10^10 -1
-341 174763 -89478480 -3.666x10^10 3
683 -349525 178956960 7.33x10^11 End of loop
So why does it loop back to 3 again?
r
Last edited:
- Joined
- Apr 22, 2007
- Messages
- 1,960
f(n)=(n-1)^2-n^2
Where N=3
Then after every full calculation N becomes the output.
First find out what happens in the output. And 2ndly explain why it does that
I've been over this before. You need to fix your notation because right now, your problem does not work. f(n) = (n - 1)2 - n2 = 1 - 2n, and there is a relatively tedious post here that explains exactly why your problem doesn't work. So please, fix it, or give input/output examples, or solve it in a spoiler tag, or something.
You'll probably say "you have to enter it in a calculator" but that makes the problem misleading and lame. Give proper notation.
- Joined
- Apr 3, 2010
- Messages
- 1,101
kk i edited. And it should work this was performed upon a scientific calculator :L
Last edited:
- Joined
- Apr 22, 2007
- Messages
- 1,960
f(n)=(n-1)^2-n^2
Basically its like this
(1-Ans)^2-ANs^2=Y
So
Here is an example
(1-3)^2-Ans^2=-5
(1--5)^2--5^2=11
(1-11)^2-11^2=-21
Etc
The following is a list of the sequence (read downwards)
3 -1365 699051 -357914000 -1.466x10^12
-5 2731 -1398101 715828000 2.93x10^12
11 -5461 2796203 -1.14532x10^10 5.86x10^12
-21 10923 -5592405 -2.2907x10^10 1.17x10^13
43 -21845 11184811 4.5814x10^10 0
-85 43691 -22369621 -9.163x10^10 1
171 -87381 44738243 1.8326x10^10 -1
-341 174763 -89478480 -3.666x10^10 3
683 -349525 178956960 7.33x10^11 End of loop
So why does it loop back to 3 again?
r
Because your calculator is bad? Limited precision? I don't know. This isn't a math problem. I could do this on my computer and I wouldn't get the same issue.
Besides, you screwed up in your output.
-2.2907*10^10 should actually be 2.8633*10^9, and all of the rest are wrong from there.
Regardless, instead of the 0, you should have -2.3456*10^13
- Joined
- Apr 3, 2010
- Messages
- 1,101
- Joined
- Apr 22, 2007
- Messages
- 1,960
Okay obvs you dont understand me i have made a vbs programn inputting the equasion for you and outputting numbers up to a point. As i did not bother looping it.
To quit off of it just go CTRL Shift Delete then close the process wscript
... I get it. In fact, I had already derived a formula to the nth output:
f(n) = 1/3 + (-2)n*8/3
So, that's how I saw that your output was wrong.
- Joined
- Apr 3, 2010
- Messages
- 1,101
Did you even loook at the programN >.<?
And no that function makes no sense its a simple
swap where
(1-Ans)^2 ALways returns a positive
And
Ans^2 always returns a positive
So therefore the change is due to a Positive-Positive which becomes less than 0 or a negative
Or when a positive -- a negative thus becoming a greater positive.
I dont see how f(n) = 1/3 + (-2)n*8/3
has any relation
As
F(1)=1/3+(-2)*8/3=1/3+-2=-1.66*8/3=4.42666667
Which fails to meat the basics requirements of a 1 start for the actual equasion starts at 0 from the loop and i gave a mid term
And no that function makes no sense its a simple
swap where
(1-Ans)^2 ALways returns a positive
And
Ans^2 always returns a positive
So therefore the change is due to a Positive-Positive which becomes less than 0 or a negative
Or when a positive -- a negative thus becoming a greater positive.
I dont see how f(n) = 1/3 + (-2)n*8/3
has any relation
As
F(1)=1/3+(-2)*8/3=1/3+-2=-1.66*8/3=4.42666667
Which fails to meat the basics requirements of a 1 start for the actual equasion starts at 0 from the loop and i gave a mid term
- Joined
- Apr 22, 2007
- Messages
- 1,960
Yeah I did. What exactly is it supposed to show? Would you like me to write one that doesn't screw up the output because of precision errors?
EDIT: Uhhh, dude, that's an exponent.
f(n) = 1/3 + (-2)n*8/3
f(0) = 1/3 + 1*8/3 = 9/3 = 3
f(1) = 1/3 + (-2)*8/3 = -15/3 = -5
f(2) = 1/3 + (-2)2*8/3 = 1/3 + 4*8/3 = 33/3 = 11
etc.
I formally derived how this equation works. It works.
EDIT: Uhhh, dude, that's an exponent.
f(n) = 1/3 + (-2)n*8/3
f(0) = 1/3 + 1*8/3 = 9/3 = 3
f(1) = 1/3 + (-2)*8/3 = -15/3 = -5
f(2) = 1/3 + (-2)2*8/3 = 1/3 + 4*8/3 = 33/3 = 11
etc.
I formally derived how this equation works. It works.
- Joined
- Apr 3, 2010
- Messages
- 1,101
:L But that doesnt explain -1 and 1 :L Also if its about precision what do you suggest i use to calculate? And C++ is not an option due to faulty Windows
Also 2.33 * 8 = 18.66664 not -15 so i wonder when u got that from :L
Also 2.33 * 8 = 18.66664 not -15 so i wonder when u got that from :L
- Joined
- Dec 12, 2008
- Messages
- 7,385
Ok guys, I wrote that problem a month ago, so I forgot the actual answer 
Here's a new one:
f(11) = 56
f(9) = 22
f(8) = 14
f(2) = 2
Can you find f(12)? ^^
Let's just say that this problem is best solved using recursion in programming and it causes an exponential growth in the number of function calls ^^
Here's a new one:
f(11) = 56
f(9) = 22
f(8) = 14
f(2) = 2
Can you find f(12)? ^^
Let's just say that this problem is best solved using recursion in programming and it causes an exponential growth in the number of function calls ^^
- Joined
- Apr 22, 2007
- Messages
- 1,960
Ok guys, I wrote that problem a month ago, so I forgot the actual answer
Here's a new one:
f(11) = 56
f(9) = 22
f(8) = 14
f(2) = 2
Can you find f(12)? ^^
Let's just say that this problem is best solved using recursion in programming and it causes an exponential growth in the number of function calls ^^
Answer is 594/7. Using the same technique as here. Pretty straightforward.
WolframAlpha, Google, Maple, matlab, anything that doesn't have terrible precision. Also, what are you talking about -1 and 1?Brambleclaw said::L But that doesnt explain -1 and 1 :L Also if its about precision what do you suggest i use to calculate? And C++ is not an option due to faulty Windows
Dude.Brambleclaw said:Also 2.33 * 8 = 18.66664 not -15 so i wonder when u got that from :L
1/3 + (-2)*8/3 = 1/3 - 16/3 = (1 - 16)/3 = -15/3 = -5
- Joined
- Apr 3, 2010
- Messages
- 1,101
I forgot bidmass :L
- Joined
- Dec 12, 2008
- Messages
- 7,385
Answer is 594/7. Using the same technique as here. Pretty straightforward.
Nope.
Math isn't about calculations and shit, it's about Trial and Error, Dumb Luck, etc..
That's what makes it fun sometimes
In that sequence, I used the fibonacci series and just added one xD
The function cant be represented mathematically, but here's what it looks like in C++
Code:
int fibonacci(int i) {
if (i==0)
return 0;
else if (i==1)
return 1;
else
return fibonacci(i-1) + fibonacci(i-2);
}
// This is the actual function
int f(int i) {
return 1 + fibonacci(i);
}lol I'm so used to programming xD
f(0) is the first number in the fibonacci series + 1
f(1) is the second number in the fibonacci series + 1
etc..
f(12) = 90
- Joined
- Apr 22, 2007
- Messages
- 1,960
Nope.
Math isn't about calculations and shit, it's about Trial and Error, Dumb Luck, etc..
That's what makes it fun sometimes
In that sequence, I used the fibonacci series and just added one xD
The function cant be represented mathematically, but here's what it looks like in C++
Code:int fibonacci(int i) { if (i==0) return 0; else if (i==1) return 1; else return fibonacci(i-1) + fibonacci(i-2); } // This is the actual function int f(int i) { return 1 + fibonacci(i); }
lol I'm so used to programming xD
f(0) is the first number in the fibonacci series + 1
f(1) is the second number in the fibonacci series + 1
etc..
f(12) = 90
Well you should have given more details, because my answer is appropriate too.
Also, that would be the Fibonacci sequence, and there is a closed-form solution for Fn:
Fn = (φn - (-φ)-n)/√5,
where φ = (1 + √5)/2
I can show you how this is, if you like. The technique I know to show it is pretty cool, and has some CS implications.
- Joined
- Aug 2, 2008
- Messages
- 219
Ok how abouot this.
"Find a power sereis which describes the indefinite antiderivate of the function f(x) = x^x."
I know this really silly and pointless, since this is that kind of function can not be represented trough any other kind of special or elementary function. But when i get bored i work out those kind of things.
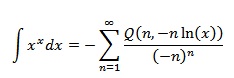 Where Q is the regularized gamma function of the lower limit which is usually defined as
Where Q is the regularized gamma function of the lower limit which is usually defined as
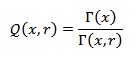 Also i worked out a n-ary sum if x is a natural number
Also i worked out a n-ary sum if x is a natural number
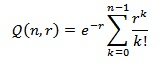
"Find a power sereis which describes the indefinite antiderivate of the function f(x) = x^x."
I know this really silly and pointless, since this is that kind of function can not be represented trough any other kind of special or elementary function. But when i get bored i work out those kind of things.
Attachments
- Joined
- Apr 22, 2007
- Messages
- 1,960
Ok how abouot this.
"Find a power sereis which describes the indefinite antiderivate of the function f(x) = x^x."
I know this really silly and pointless, since this is that kind of function can not be represented trough any other kind of special or elementary function. But when i get bored i work out those kind of things.
Where Q is the regularized gamma function of the lower limit which is usually defined as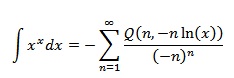
Also i worked out a n-ary sum if x is a natural number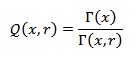
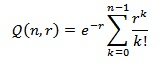
This thread just leveled up.
- Joined
- Aug 2, 2008
- Messages
- 219
This thread just leveled up.
You think so ? Solving that thing is not really as hard as it looks like.
Just rewrite xx with its exponential form ex*ln(x) and replace the ex with its taylor series. Then try to integrate the series by turning it into a recursive equation. Once you have the recursive equation you can transform it into an n-ary sum and compare that sum with the incomplete gamma function. Then do some adjustments and you can express the recursive equation in terms of the incomplete gamma function. When you did that just put the gamma expression back into the taylor series of the exponential function and you got the rough form of my sum.
- Status
- Not open for further replies.
Similar threads
- Replies
- 13
- Views
- 2K
- Replies
- 9
- Views
- 2K
- Replies
- 2
- Views
- 988


















