Mathematics thread

[Nuclear]

Post math related questions, answer them etc.

I'll start (not a homework question, I swear):

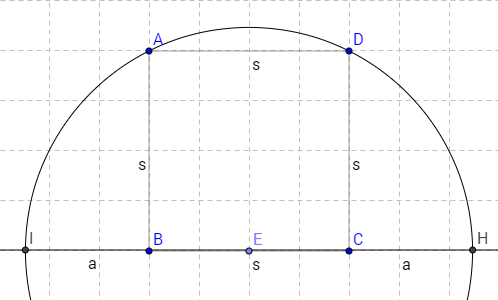
Solve the relation of s and a (s/a,see the picture).

Also feel free to post homework questions if you're a lazy bastard.

edit: fixed the picture

 

[Mechanical Man]

Shouldn't be s equal everywhere? Now you have one s side being 6 squares long, other side being 5 and something squares long.

 

[Nuclear]

The graphical representation is inaccurate and only intended for easier understanding of the question. So yes, the sides are equal and its corners are touching the half circle's edge.

Here's a fixed version anyway:

If nobody comes up with anything I'll try to solve it myself tomorrow.

 

[GhostThruster]

a = sqrt(5)*s/2

 

[Nuclear]

Looks right, but the point was to explain how you got the solution, not just posting it.

 

[GhostThruster]

Ok ED = EH = a
By pythy's theorem, ED^2 = EC^2 + CD^2
. : a^2 = (s/2)^2 + s^2
Then root both sides, group under common denominator

 

[PurplePoot]

Fun one if someone wants a challenge:

Consider the set C_k consisting of all k-tuples of subsets of N = {1..n} which satisfy the following property:

∀e ∈ C_k, e = (a₁,...,a_k) such that ∀i 0≤i≤k, a_i ⊆ N
a_2i-1 ⊆ a_2i ⊇ a_2i+1 ∀i (for indices ≤ k)

Give (and justify) an expression for |C_k| given n and k.

Edit: A hint to get people started. Let's prove k = 1 (which is equivalent to the power set problem). You probably know how to prove this already if you're attempting this problem, but you may not have seen this approach before:

Hint

Stuff we'll need - Rules of arithmetic:

1. There exists a bijection from S to T if and only if |S| = |T|
2. If S∩T = ∅, then |S∪T| = |S| + |T| (disjoint union)
3. |SxT| = |S||T| (set cross product)

Corollary: Define the nth power of a set Sⁿ as Sx...xS (n times). |Sⁿ| = |S|ⁿ

The proof:

Let V_n be the set of all binary vectors of length n.

Claim: There is a bijection from V_n to C₁

Proof: Elements in N are either included or excluded in every a ∈ C₁. Let 0 represent exclusion and 1 represent inclusion. We have |N| = n, and |a| = n, so let each element in a correspond to a unique element in N. Therefore there is a clear bijection between V_n and C₁.

We have V_n = {0,1}ⁿ. Therefore:
|V_n| = |{0,1}ⁿ|
|V_n| = |{0,1}|ⁿ (By rule 3)
|V_n| = 2ⁿ
|V_n| = |C₁| (By rule 1)
|C₁| = 2ⁿ

 

[fladdermasken]

A town with a population of n has m clubs such that

• Each club has an odd number of members.
• Any two clubs have an even number of shared members.

Show that m ≤ n.

Hint: This problem is easier if you think of each club as a vector.

a_2i-1 ⊆ a_2i ⊇ a_2i+1 ∀i (for indices ≤ k)

Just to be clear, considering people keep switching the notations around, by ⊆ and ⊇ you mean subset and superset respectively, right? Also we can't assume they're proper subsets/supersets?

 

[Nuclear]

Ok ED = EH = a
By pythy's theorem, ED^2 = EC^2 + CD^2
. : a^2 = (s/2)^2 + s^2
Then root both sides, group under common denominator

Oh, actually a = CH = IB, not the whole radius of the circle.

 

[PurplePoot]

Just to be clear, considering people keep switching the notations around, by ⊆ and ⊇ you mean subset and superset respectively, right? Also we can't assume they're proper subsets/supersets?

Yes. Basically each even-indexed subset contains the odd-indexed subsets on either side of it. And all subsets in this question are improper.

Edit: fladdermasken, this is more of a statement of truth than a proof given how rusty my linear algebra is, but my answer to yours is that it's equivalent to linear independence. Construct n one-member clubs and it's clear that you can't add any more. You can easily make the clubs larger but if you treat clubs as initially one-entry vectors which grow as you add members to them it's clear that even though you can grow existing clubs you'll never be able to add any new ones.

 

[fladdermasken]

Another fun problem for the layman is one in HINDYhat's old maths thread.

Which is greater, the number of naturals or the number of squares of naturals? Note that for every natural number n, there is a corresponding square n², but some natural numbers, e.g. 2 and 3, are not the squares of natural numbers.

If you don't know the natural numbers, that would be the set {0, 1, 2, ...}.

Yes. Basically each even-indexed subset contains the odd-indexed subsets on either side of it. And all subsets in this question are improper.

I'll have to think that one over. Pretty tricky.

fladdermasken, this is more of a statement of truth than a proof given how rusty my linear algebra is, but my answer to yours is that it's equivalent to linear independence. Construct n one-member clubs and it's clear that you can't add any more. You can easily make the clubs larger but if you treat clubs as initially one-entry vectors which grow as you add members to them it's clear that even though you can grow existing clubs you'll never be able to add any new ones.

Essentially, yes. The conditions imply linear independance over the field F₂ where 1 + 1 = 0, i.e. odd is one and even is zero. I'll leave the rest of the proof in the hidden tag if someone wants to attempt it, but you have pretty much all you need there.

Proof

We claim that v₁, v₂, ..., v_n is linearly independant over F₂.

Let λ₁v₁ + λ₂v₂ + ... + λ_mv_m = 0.

Then for every i

0	= (λ1v1 + λ2v2 + ... + λmvm)Tvi
= λ1v1Tvi + λ2v2Tvi + ... + λmvmTvi
= λi

Ergo m ≤ n, because the vectors are linearly dependant in a an n-dimensional space.

Q.E.D

 

[PurplePoot]

I added a proof for k = 1 which may give you some ideas.

Which is greater, the number of naturals or the number of squares of naturals? Note that for every natural number n, there is a corresponding square n², but some natural numbers, e.g. 2 and 3, are not the squares of natural numbers.

This one is pretty easy for anyone with some set theory. I'll leave it in a hidden tag in case anyone else wants to attempt it.

Answer

The two sets are the same size.

Claim: There exists a bijection between N and N²

Proof: Given n ∈ N, we can produce n² ∈ N² via a square. This number is unique for n ≠ m by definition (not true for integers, but we don't have to worry about that).
Given n² ∈ N², we can produce n ∈ N via a square root. This number is unique for n ≠ m by definition (same caveat as the above).

Therefore there exists a bijection between N and N², so |N| = |N²|.

 

[Moy]

Calculate the exact value of Pi.

Hope you'll answer me, I hate rounded numbers I want an exact one.

 

[LordDz]

The exact value?
Sure, here:

 

[Moy]

Congratulations you've answered my question correctly. But I was expecting a "pie".